
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Лекция 3 - численные методы
|
|
|
|
Свойства пространства и времени. Проблема размерности пространства и времени. Качественное многообразие форм пространства и времени в неживой природе. Биологическое и социальное пространство и время.
Понятия пространство и времени. Субстанциальная и реляционная концепции пространства и времени. Теория относительности А. Эйнштейна и идея связи материи, движения, пространства и времени.
Обсуждение вопроса о сущности пространства и времени в истории философии распадается на три группы проблем: 1. Каков гносеологический статус этих понятий? Являются ли они характеристиками материального бытия или характеризуют устройство нашего сознания? 2. Каково отношение пространства и времени к субстанции? 3. Каковы основные свойства пространства и времени?
Вопрос о познавательном статусе пространства и времени решался по-разному. Одни философы считали пространство и время объективными характеристиками бытия, другие - чисто субъективными понятиями, характеризующими наш способ восприятия мира. Были философы, которые, признавая объективность пространства, приписывали чисто субъективный статус категории времени, и наоборот.
Но пространство и время являются столь же объективными характеристиками бытия, как его материальность и движение.
В истории философии существовали две точки зрения об отношении пространства и времени к материи. Первую из них можно условно назвать субстанциальной концепцией. В ней пространство и время трактовали как самостоятельные сущности. существующие наряду с материей и независимо от нее. Соответственно отношение между пространством, временем и материей представлялось как отношение между двумя видами самостоятельных субстанций. Это вело к выводу о независимости свойств пространства и времени от характера протекающих в них материальных процессов.
Вторую концепцию можно именовать реляционной (от слова “relatio“ - отношение). Ее сторонники понимали пространство и время не как самостоятельные сущности, а как системы отношений, образуемых взаимодействующими материальными объектами. Вне этой системы взаимодействий пространство и время считались несуществующими. В этой концепции пространство и время выступали как общие формы координации материальных объектов и их состояний. Соответственно допускалась и зависимость свойств пространства и времени от характера взаимодействия материальных систем.[1] С точки зрения признания объективности пространства и времени обе этих концепции равноценны. Если говорить об их естественнонаучной обоснованности, то в 17-19 веках явное преимущество было на стороне субстанциальной концепции; именно она лежала в основе ньютоновской механики, принимавшейся в то время за образец точной науки. Сильнейшим свидетельством в пользу субстанциальной концепции пространства был факт единственности евклидовой геометрии. Хотя еще в 30-х гг. 19 века Лобачевским была открыта неэвклидова геометрия, до открытия общей теории относительности, неэвклидовы геометрии рассматривались как воображаемые математические конструкции, и им не приписывалось реального физического смысла. Единственной геометрией, описывающей реальные свойства физического пространства и времени, считалась геометрия Евклида. А это как бы подтверждало вывод, следовавший из субстанциальной концепции, что свойства пространства и времени неизменны и независимы от характера движения и взаимодействия материальных систем.
Пространство и время представляют собой формы, выражающие определенные способы координации материальных объектов и их состояний. Содержанием этих форм является движущая материя, материальные процессы, и именно особенности и характер последних должны определять их основные свойства. В этом отношении диалектика нацеливала науку на поиски зависимости между определенными свойствами пространства и времени и сопутствующими материальными процессами. которые их определяют. Кроме того, наличие у пространства и времени единого содержания - движущей материи - указывает и на взаимосвязь между самим пространством и временем, на невозможность их существования абсолютно независимо друг от друга.
В начале 20 века была создана теория относительности, которая заставила пересмотреть традиционные воззрения на пространство и время и отказаться от субстанциальной концепции. Теорию относительности можно рассматривать как концепцию, нацеленную на раскрытие диалектических связей в природе.
Теория относительности включает в себя две генетически связанные теории: специальную теорию относительности (СТО), основные идеи которой были сформулированы А. Эйнштейном в 1905 году, и общую теорию относительности (ОТО), работу над которой Эйнштейн закончил в 1916 году.
СТО возникла как результат попыток Эйнштейна распространить действие физического принципа относительности на законы электродинамики, которые рассматривались как противоречащие последнему. В результате пришлось пересмотреть ньютоновские пространственно-временные представления. СТО показала, что многие пространственно-временные свойства, считавшиеся до сих пор неизменными, абсолютными, фактически являются релятивными. Так, в СТО утратили свой абсолютный характер такие пространственно-временные характеристики, как длина, временной интервал, понятие одновременности. Все эти характеристики оказываются зависящими от взаимного движения материальных объектов.
Новые подтверждения правильности реляционной концепции пространства и времени дала ОТО. Если в СТО принцип относительности был связан только с инерциальными системами отсчета, то общая теория относительности явилась результатом распространения действия принципа относительности и на неинерциальные системы отсчета. Это привело к установлению тесной зависимости метрических свойств пространства-времени от гравитационных взаимодействий между материальными объектами. В СТО было установлено, что геометрические свойства пространства-времени зависят от распределения в них гравитационных масс. Вблизи тяжелых объектов геометрические свойства пространства начинают отклоняться от евклидовых, а темп течения времени замедляется. ОТО нанесла удар по субстанциальной концепции пространства и времени.
Основное философское значение теории относительности состоит в следующем: 1. Теория относительности исключила из науки понятия абсолютного пространства и абсолютного времени, обнаружив тем самым несостоятельность субстанциальной трактовки пространства и времени как самостоятельных, независимых от материи форм бытия. 2. Она показала зависимость пространственно-временных свойств о характера движения и взаимодействия материальных систем, подтвердила правильность трактовки пространства и времени как основных форм существования материи, в качестве содержания которых выступает движущая материя. Сам Эйнштейн, отмечая на заданный ему вопрос о сути теории относительности, сказал: “Суть такова: раньше считали, что если каким-нибудь чудом все материальные вещи исчезли бы вдруг, то пространство и время остались бы. Согласно же теории относительности вместе с вещами исчезли бы пространство и время”. 3. Теория относительности нанесла удар субъективистским, априористским трактовкам сущности пространства и времени, которые противоречили ее выводам.
Общие свойства, характеризующие пространство и время, вытекают из их характеристик как основных, коренных форм существования материи. К свойствам пространства относятся протяженность, однородность и изотропность, трехмерность. Время обычно характеризуется такими свойствами, как длительность, одномерность, необратимость, однородность.
Что касается таких свойств, как длительность времени и протяженность пространства, то их трудно назвать свойствами, поскольку они совпадают с самой сущностью пространства и времени. Ведь протяженность и проявляется в способности тел существовать одно подле другого, а длительность в способности существовать одно после другого, что и выражает сущность пространства и времени как форм существования материи.
К наиболее характерным свойствам пространства относится его трехмерность. Положение любого объекта может быть определено с помощью трех независимых величин. Время одномерно, ибо для фиксации положения события во времени достаточно одной величины. Под заданием положения события, объекта в пространстве или во времени имеется в виду определение его координат по отношению к другим событиям и объектам. Факт трехмерности реального физического пространства не противоречит существованию в науке понятия многомерного пространства с любым числом измерений. Понятие многомерного пространства является чисто математическим понятием, которое может быть использовано для описания взаимосвязи различного рода физических величин, характеризующих реальные процессы. Если же речь идет о фиксации события в реальном физическом пространстве, то при использовании любой системы координат трех измерений всегда будет достаточно.
К специфическим свойствам пространства относится однородность и изотропность. Однородность пространства означает отсутствие в нем каких-либо выделенных точек, а изотропность - равноправность всех возможных направлений. В отличие от пространства время обладает только свойством однородности, заключающихся в равноправии всех его моментов. Свойства однородности пространства и времени и изотропности пространства тесно связаны с фундаментальными физическими законами, и прежде всего с законом сохранения. Они и лежат в основании самого принципа физической относительности.
Характерным специфическим свойством времени является его необратимость, которая проявляется в невозможности возврата в прошлое. Время течет от прошлого через настоящее к будущему, и обратное течение его невозможно. Необратимость времени связана с необратимостью протекания фундаментальных материальных процессов. Некоторые философы усматривают связь необратимости времени с необратимостью термодинамических процессов и с действием закона возрастания энтропии.
Специфично проявление времени пространства в микромире, живой природе, в социальной действительности, в связи с чем специально анализируется биологическое время, психологическое время, социальное пространство-время и другие виды времени и пространств.
Психологическое (перцептуальное) время связано с восприятием и переживанием времени индивидом: время то “бежит”, то “замедляется”, то зависит от тех или иных конкретных ситуаций (одно дело, когда мы кого-то ожидаем, а другое, когда заняты чем-то интересным); в детстве нам кажется, что время течет медленно, а в зрелом возрасте, что оно ускорило свой бег. Это субъективное чувство времени, и оно лишь в целом соответствует реально-физическому времени. Как отмечают специалисты, психологическое время включает оценки одновременности, последовательности, длительности, скорости протекания различных событий жизни, их принадлежности к настоящему, удаленности в прошлое или будущее, переживания сжатости и растянутости, прерывности и непрерывности, ограниченности и беспредельности времени, осознание возраста, возрастных этапов, представления о вероятной продолжительности жизни, о смерти и бессмертии, об исторической связи собственной жизни с жизнью предшествующих и последующих поколений и т.п.
Возникновение социально организованной материи связано с формированием новых пространственно-временных структур. Здесь возникает особый тип пространственных отношений, в котором воспроизводится и исторически развивается человек как общественное существо. Социальное пространство обладает особым человеческим смыслом. Оно функционально расчленено на ряд подпространств, характер которых и их взаимосвязь исторически меняются по мере развития общества. Социальное время тоже имеет сложную структуру. Оно возникает как наложение друг на друга различных временных структур. В рамках исторического времени, в котором происходят события, характеризующие историю народа, нации, развитие и смену общественно-экономических формаций, можно выделить время индивидуального бытия человека, которое определяется протеканием различных социально и индивидуально значимых для него событий.
[1] Баженов Л.Б., Морозов К.Е., Слуцкий М.С. Философия естествознания. М., 1966.
Молчанов Ю.Б. Проблема синтеза различных концепций времени // Синтез современного научного знания.
М., 1973.
Решение систем линейных уравнений.
|
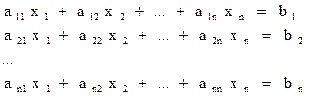 |
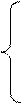 Дана система линейных уравнений (СЛУ) с n неизвестными:
Дана система линейных уравнений (СЛУ) с n неизвестными:
В матричной форме записи система (4.1) имеет вид:
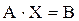 (4.2)
(4.2)
где: n – порядок системы;
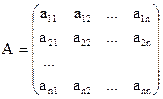 – матрица коэффициентов системы;
– матрица коэффициентов системы;
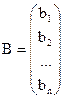 – вектор свободных членов;
– вектор свободных членов; 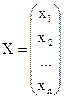 – вектор неизвестных;
– вектор неизвестных;
В свернутой форме записи СЛУ имеет вид:
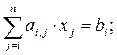
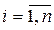 (4.3)
(4.3)
Система называется обусловленной (не вырожденной, не особенной), если определитель системы DA ¹ 0, и тогда система (4.1) имеет единственное решение.
Система называется не обусловленной (вырожденной, особенной), если DA = 0, и тогда система (4.1) не имеет решений или имеет бесконечное множество решений.
На практике коэффициенты системы aij и свободные члены bi часто задаются приближенно, с некоторой неустранимой погрешностью. Поэтому, кроме существования и единственности решения СЛУ, важно еще знать, как влияет такая погрешность на получаемое решение.
Система называется плохо обусловленной, если неустранимая погрешность оказывает сильное влияние на решение; у таких систем определитель близок, но не равен 0.
Рассмотрим пример плохо обусловленной системы.
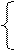 Дана система
Дана система 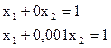
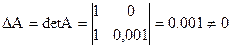
Решение 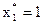 ;
; 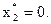
Пусть b2 имеет неустранимую погрешность 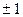 %.
%.
Если b2 = 1,01, то 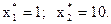
Если b2 = 0,99, то 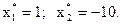
Решение изменяется очень сильно, следовательно, система плохо обусловлена, о чем говорит значение её определителя.
Рассмотрим геометрическую иллюстрацию обусловленности СЛУ на примере системы двух уравнений с двумя неизвестными:
 a11 x1+ a12 x2 = b1 уравнение (I)
a11 x1+ a12 x2 = b1 уравнение (I)
a21 x1+ a22 x2= b2 уравнение (II)
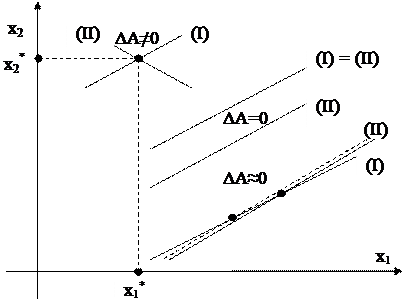 |
Рис. 3.1. Геометрическая иллюстрация обусловленности СЛУ.
Каждому уравнению в плоскости (x1,x2) соответствует прямая, а точка пересечения этих прямых является решением этой системы. Если ΔA = 0, то наклоны прямых одинаковы, и они либо параллельны (т.е. не имеют решения), либо совпадают (имеют бесконечное множество решений). Если ΔA ¹ 0, то прямые имеют единственную точку пересечения.
Но если система плохо обусловлена (∆А≈0), даже незначительное изменение одного из коэффициентов приведет к сильному изменению решения системы, т.к. прямые почти параллельны.
Для решения СЛУ широко применяться прямые и итерационные методы. Область применения некоторых из них показана в таблице.
| Тип | Название метода | Число арифметических действий (при n = 20) | Область примененения |
| Прямые | Формулы Крамера | ~ 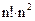 ( (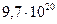 ) )
| n<5 |
| Исключения Гаусса | ~ 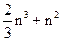 (5733) (5733)
| n<200 | |
| Итерационные | Простых итераций | ~ n² на каждой итерации (400n) | до 105 |
| Гаусса-Зейделя |
Современная супер-ЭВМ имеет производительность 30 терафлоп – 30·1012 операций с вещественными числами в секунду. Такой машине для решения СЛУ для n=20 по формуле Крамера требуется:
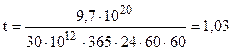 года.
года.
На решение СЛУ прямым методом сильное влияние оказывает погрешность округления, т.к. требуется огромное количество арифметических действий.
На решение СЛУ итерационным методом погрешность округления практически не влияет, но не всегда удается обеспечить сходимость итерационного процесса.
3.1. Формулы Крамера.
xi* = DAi / DA, i = 1, n, 1 (4.4)
где Ai – вспомогательная матрица, полученная из A заменой i-го столбца вектором свободных членов.
Пример 4.1. Решить СЛУ, используя формулы Крамера.
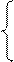 x1 + 5×x2 - x3 = 2
x1 + 5×x2 - x3 = 2
x1 2×x3 = -1
2×x1 - x2 – 3×x3 = 5
Вычислим определители по правилу треугольников:
DA = 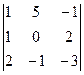 = 0 + 1 + 20 + 0 + 15 + 2 = 38 – система обусловлена.
= 0 + 1 + 20 + 0 + 15 + 2 = 38 – система обусловлена.
DA1 = 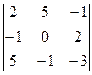 = 0 + 50 - 1 - 0 + 4 - 15 = 38
= 0 + 50 - 1 - 0 + 4 - 15 = 38
DA2 = 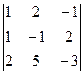 = 3 + 8 – 5 – 2 + 6 - 10 = 0
= 3 + 8 – 5 – 2 + 6 - 10 = 0
DA3 = 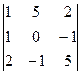 = 0 - 10 – 2 – 0 -25 - 1 = -38
= 0 - 10 – 2 – 0 -25 - 1 = -38
Вычислим решения:
x1* = DA1 / DA = 38/38 = 1;
x2* = DA2 / DA = 0/38 = 0;
x3* = DA3 / DA =-38/38 = -1.
Проверим полученное решение подстановкой в исходную систему.
1 + 5×0 – (-1) = 2
1 + 2×(-1) = -1
2×1 – 0 – 3×(-1) = 5
Система обращается в тождество, решение верное.
Формулы Крамера применяться редко, только для n≤4.
3.2. Метод исключений Гаусса.
Решим рассмотренную ранее систему (пример 4.1) методом исключения Гаусса.
Пример 3.2. Решение проводиться в два этапа.
1 этап Прямой ход - матрица A преобразуется к треугольному виду: путем эквивалентных линейных преобразований уравнений системы поддиагональные коэффициенты матрицы А обнуляются.
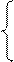 x1 + 5×x2 - x3 = 2
x1 + 5×x2 - x3 = 2
x1 2×x3 = -1
2×x1 - x2 – 3×x3 = 5
Исключим x1 из 2-го и 3-го уравнения: ко 2-му уравнению прибавим 1-ое, умноженное на (-1); к 3-му уравнению прибавим 1-ое, умноженное на (-2).
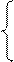 x1 + 5×x2 - x3 = 2
x1 + 5×x2 - x3 = 2
- 5×x2 + 3×x3 = -3
- 11×x2 – x3 = 1
Исключим x2 из 3-го уравнения: к 3-му уравнению прибавим 2-ое, умноженное на (-11/5). Полученный вид системы после прямого хода
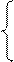 x1 + 5×x2 - x3 = 2
x1 + 5×x2 - x3 = 2
- 5×x2 + 3×x3 = -3
– 38/5×x3 = 38/5
2 этап Обратный ход - вычисляются значения неизвестных, начиная с последнего уравнения:
x3* = -1
-5×x2 + 3×x3*=-3 Þ x2*=(3 + 3×x3*)=(3 + 3×(-1))=0
x1 +5×x2* - x3*=2 Þ x1*=2 + 5×x2* + x3*=2 + 5×0 + (-1)=1
Полученное решение нужно обязательно проверить, подставив в исходную систему!
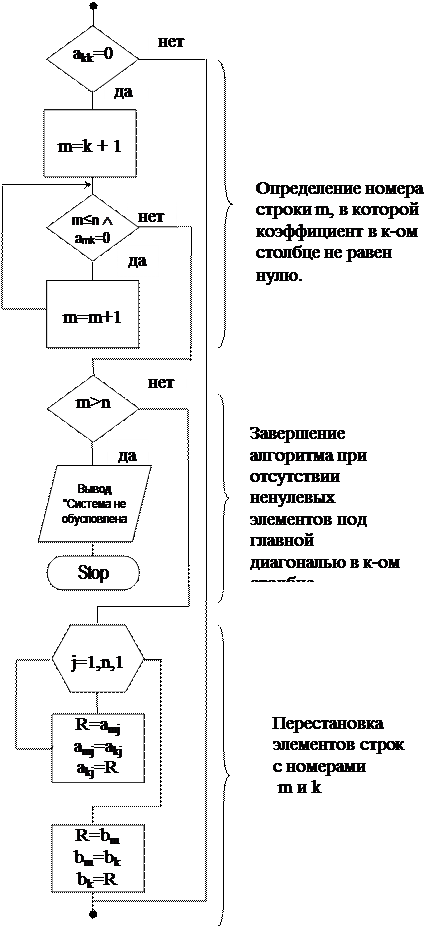
Словесное описание алгоритма метода исключения Гаусса. Схема алгоритма приведена на рисунках 4.1-4.6.
Алгоритм прямого хода:
Шаг 1. Примем k=1
Шаг 2. Выбираем рабочую строку.
Если akk ≠ 0, то k-ая строка – рабочая.
Если нет, меняем k-ю строку на m-ю (n≥m>k), в которой amk ≠ 0, 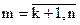 . Если такой строки нет, система вырожденная, решение прекратить.
. Если такой строки нет, система вырожденная, решение прекратить.
Шаг 3. Для строк i=k+1, k+2, …, n вычисляются новые значения коэффициентов.
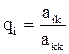 ,
, 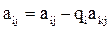 ,
, 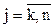 и новые правые части
и новые правые части 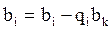
Шаг 4. Увеличиваем k = k + 1. Если k = n, прямой ход завершен, иначе алгоритм повторяется со второго шага.
Получаем верхнюю треугольную матрицу А:
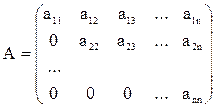 ,
, 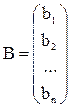
Алгоритм обратного хода:
Шаг 1. Вычислим 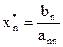
Шаг 2. Вычислим:
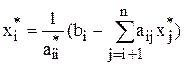 ,
, 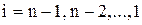
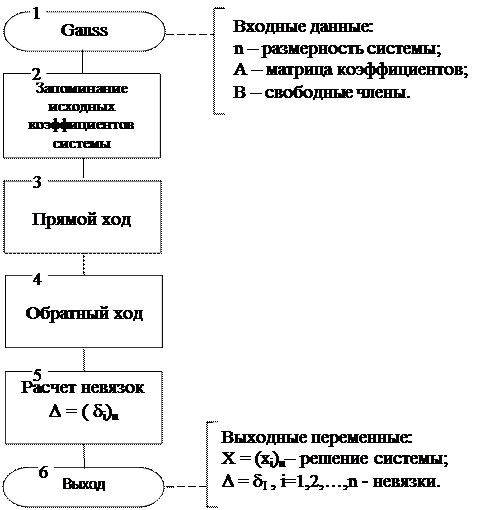 Основной алгоритм решения СЛУ методом исключения Гаусса.
Основной алгоритм решения СЛУ методом исключения Гаусса.
Рис. 3.1. Основной алгоритм решения СЛУ методом исключения Гаусса.
Для контроля правильности решения нужно считать невязки δi по формуле (4.5).
δi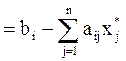 ,
, 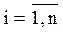 (4.5)
(4.5)
Если невязки велики, задача решена неверно. Причиной может быть сбой машины (крайне редко), ошибки в программе, погрешность округления (при большом n и когда DA = detA = 0- система плохо обусловлена).
Разновидности метода исключения:
а) Метод исключения Гаусса с выбором главного элемента в столбце.
В алгоритме прямого хода на шаге 2 рабочая строка выбирается из условия
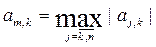 ,
,
т.е. рабочей выбирается та строка, в которой находится наибольший по модулю коэффициент k-го столбца, расположенный на главной диагонали и под ней.
б) Метод Гаусса-Жордана.
В алгоритм прямого хода нужно внести следующие изменения:
- на шаге 3 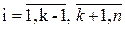
- на шаге 4 прямой ход завершиться при достижении условия k>n.
Вид матрицы коэффициентов после прямого хода
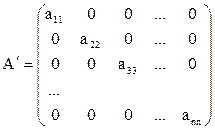
Упрощается обратный ход: xi =bi / ai,i, i =1,2,…,n
Недостаток метода – увеличение общего числа действий, и соответственно, влияния погрешности округления.
 | |||
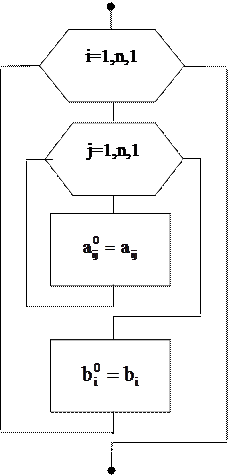 | |||
Рис. 3. Алгоритм запоминания коэффициентов.
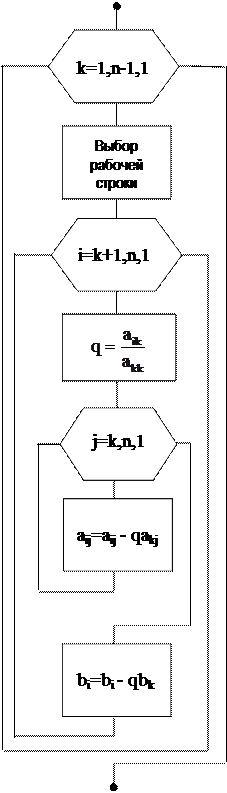
Рис. 3.2. Алгоритм прямого хода
 | |||
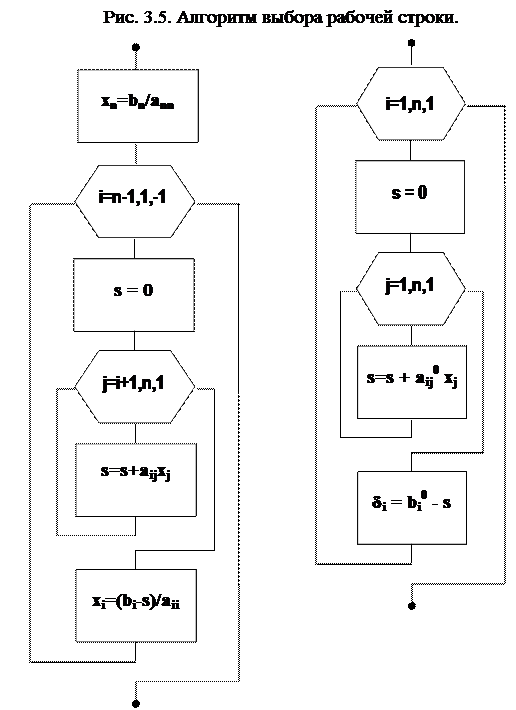 |
Рис. 4.6. Алгоритм расчета невязок
Рис. 3.5. Алгоритм обратного хода.
Нужно подчеркнуть, что для вычисления значения определителя квадратной матрицы можно использовать алгоритм прямого хода: для треугольной или диагональной квадратной матрицы определитель равен произведению элементов главной диагонали.
4.3. Метод простых итераций.
Рассмотрим особенности решения СЛУ методом простых итераций на примере.
Пример 4.3. Требуется найти решение системы с точностью ε=0,001.
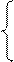 x1 + 5×x2 - x3 = 2
x1 + 5×x2 - x3 = 2
x1 2×x3 = -1
2×x1 - x2 – 3×x3 = 5
Приведем систему к новому, каноническому виду метода простых итераций. Для этого нужно преобразовать исходную систему так, чтобы в каждой строке новой матрицы А коэффициент, расположенный на главной диагонали, превышал по абсолютной величине сумму абсолютных значений остальных коэффициенты в этой сроке.
При выполнении эквивалентных линейных преобразований системы нужно соблюдать следующие требование: каждое уравнение исходной системы должно участвовать хотя бы в одном преобразовании.
В первом уравнении исходной системы коэффициент при х2 больше суммы модулей других коэффициентов: 5> 1+1. Поэтому это уравнение в новой системе нужно записать вторым уравнением. Для получения нового первого уравнения можно второе уравнение умножить на 2 и сложить с третьим уравнением. Для получения нового третьего уравнения можно из третьего уравнения вычесть второе.
В итоге описанных преобразований получиться следующая система:
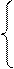
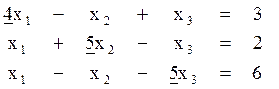
Важно отметить, что подобные преобразования не меняют решения системы.
Выразим явно из каждого нового уравнения очередное неизвестное – получим формулы итерационного процесса.
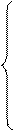
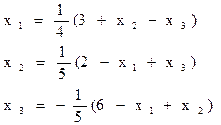
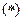
Возьмем любое начальное приближение 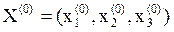 , например
, например 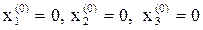 .
.
Вычислим новое приближение решения 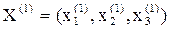 , подставив в правую часть
, подставив в правую часть 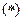 начальное приближение:
начальное приближение:
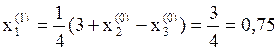
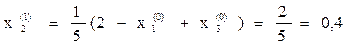
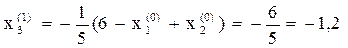
Оценим достигнутую точность δ по формуле:
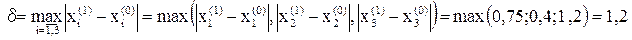
Итерационный процесс нужно продолжить, т.к. δ > ε.
Вычислим второе приближение 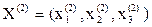 , подставив в правую часть
, подставив в правую часть 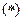 первое приближение:
первое приближение:
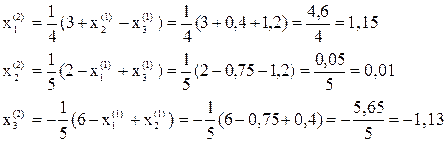
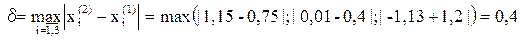
Третье приближение:
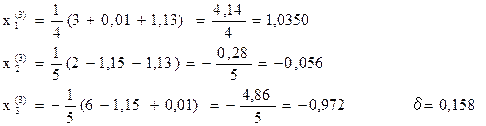
Четвертое приближение:
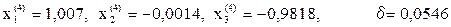
Очевидно, что итерационный процесс сходиться, т.к. значение δ монотонно убывает. Для достижения требуемой точности ε=0,001 потребуется еще несколько итераций.
Скорость сходимости зависит от уровня преобладания значений диагональных коэффициентов.
Основные расчетные зависимости метода простых итераций:
Формула итерационного процесса:
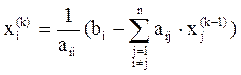 ,
, 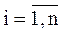 (3.6)
(3.6)
где: k = 1, 2, … – номер приближения.
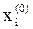 – начальное приближение,
– начальное приближение, 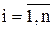 ;
;
Условия завершения итерационного процесса:
d£e (3.7)
где e – требуемая точность;
d – оценка достигнутой точности, 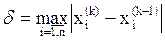 (3.8)
(3.8)
или 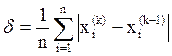 (3.9)
(3.9)
Условие сходимости итерационного процесса (условие преобладания диагональных коэффициентов):
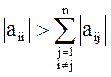
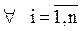 (3.10)
(3.10)
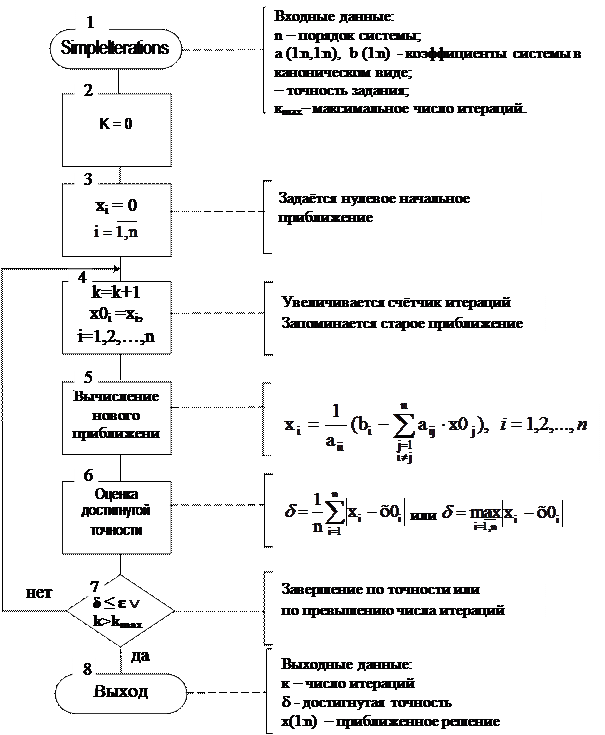
Схема алгоритма метода представлена на рис. 4.7.
Если в полученных результатах значения δ > e и k > kmax, то задача не решена, т.е. x(1:n) не является решением системы. Необходимо проверить условия сходимости или увеличить kmax.
3.4 Метод Гаусса-Зейделя
В формуле итерационного процесса метода простых итераций (4.6) к моменту вычисления xi(k) уже вычислены значения x1(k),x2(k),...,xi-1(k).
Очевидно, что эти значения в большинстве случаев ближе к решению и их можно использовать для вычисления xi(k). Исходя из этого, Гаусс и Зейдель предложили видоизмененную формулу итерационного процесса
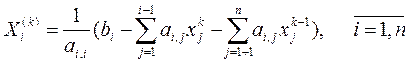 (3.11)
(3.11)
Условие завершения итерационного процесса (4.7) и условия сходимости (4.10) справедливы и для данного метода. Поэтому схема алгоритма Гаусса-Зейделя отлична только формулой расчета нового приближения:
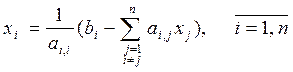
Метод этот, как правило, позволяет достичь требуемой точности ε за меньшее число итераций, т.е. имеет лучшую сходимость.
Достоинства итерационных методов:
1. Погрешность округления не накапливается от итерации к итерации.
2. Число итераций при n>100 обычно меньше n, поэтому общее число действий меньше n3, т.е. меньше, чем в методе исключений Гаусса.
3. Не требуется больший объем памяти.
4. Итерационные методы особенно выгодны для систем с большим количеством нулевых коэффициентов (систем с разряженной итерацией). Методы исключения наоборот: чем больше нулей, тем чаще требуется выбирать новую рабочую строку.
Недостаток - не всегда можно обеспечить сходимость итерационного процесса. С увеличением размерности системы труднее выполнить линейные преобразования для обеспечения сходимости.
 |
|
|
|
|
Дата добавления: 2014-01-20; Просмотров: 634; Нарушение авторских прав?; Мы поможем в написании вашей работы!