Модели с латентными переменными

Вероятностные модели.

Стохастические модели

Многомерное шкалирование (МШ).

Одним из количественных методов изучения психических явлений и процессов, адекватно отражающих их системный характер, признан метод МШ. С его помощью анализируются попарные различия D_ij между элементами i и j, в результате чего строится геометрический образ системы. Элементы системы изображаются точками моделирующего пространства, а связям между элементами соответствуют расстояния d_ij между i и j. Метод МШ разрабатывался в работах У.Торгерсона, Р.Шеппарда, К.Кумбса, Д.Краскала, Ф.Янга, В.Крылова и других.

Модели МШ можно расклассифицировать по двум основаниям.

По типу данных, полученных в эксперименте:

§ прямое субъективное шкалирование (задана одна матрица близостей Dij);

§ модель предпочтений (задана матрица близостей D_ij и матрица предпочтений);

§ модель индивидуального шкалирования (задано несколько матриц близостей).

По процедуре реализации метода:

§ метрическое шкалирование (расстояние в реконструируемом пространстве d_ij пропорционально различиям D_ij, полученным в эксперименте);

§ неметрическое шкалирование (данные D_ij монотонно связаны с расстояниями d_ij в пространстве Минковского).

Совместное использование МШ и КА позволяет провести анализ данных, более адекватный, чем даёт применение каждого метода в отдельности. При больших выборках необходимо сначала провести КА, а затем, с помощью МШ реконструировать пространство всех классов и каждого класса в отдельности (при необходимости). На основании обобщённого опыта было обнаружено, что при КА маленькие классы адекватны данным, часто являясь осмысленными группами, а большие – нет. И, наоборот, при МШ небольшие изменения в данных могут стать причиной существенных изменений в локальном взаимном расположении точек. В то же время общее расположение точек внутри конфигурации является содержательным (см. работы Граева, Суппеса).

Модели с латентными переменными являются важным классом вероятностных моделей. Они основаны на предположении о том, что наблюдаемые, объясняемые тестами переменные могут быть объяснены с помощью так называемых латентных более глубинных переменных, которые невозможно измерить непосредственно, однако можно оценить их значение косвенно. К методам латентных переменных относятся:

§ конфирматорный факторный анализ,

§ эксплораторный факторный анализ,

§ регрессионный анализ,

§ однофакторный анализ,

§ методы латентных структур.

Цель создания моделей с латентными переменными – объяснение наблюдаемых переменных и взаимосвязей между ними с помощью латентных переменных. При заданном значении наблюдаемых переменных требуется сконструировать множество латентных переменных и функцию, которая достаточно хорошо аппроксимировала бы наблюдаемые переменные, а в конечном счёте – плотность вероятности наблюдаемой переменной.

В факторном анализе основной акцент делается на моделировании значений наблюдаемых переменных, их корреляциях, ковариациях, а в методах латентно-структурного анализа – на моделировании распределения вероятности наблюдаемых переменных.

Модели факторного анализа (ФА).

Работа Пирсона (1901) – первая, которая была посвящена методу главных компонент. Большой вклад при разработке теста на интеллект внесли К.Спирмен (1926, 1946), Л.Тёрстон (1947, 1951), а при разработке теории личности – Р.Кеттел (1947, 1951) и Г.Ю.Айзенк.

Входные данные, обрабатываемые методом ФА, - это корреляционная или ковариационная матрицы. Основная цель – выявление интегральных латентных факторов по наблюдаемым переменным, что означает построение для данной корреляционной матрицы K соответствующей матрицы нагрузок A. Матрица А определяется численными методами, при этом количество факторов не должно превышать количество наблюдаемых переменных. То есть соотношение между n наблюдаемыми переменными должны объясняться возможно меньшим числом латентных факторов.

Первый принцип, лежащий в основе классической модели ФА, - постулат о линейной независимости между линейными характеристиками;

Второй – наблюдаемые переменные могут быть представлены как линейная комбинация некоторых латентных факторов. Ряд этих факторов является общим для нескольких переменных, другие – специфические, связанные, в основном, только с одной переменной.

В 60-е годы, в связи с быстрым развитием методов ФА, появилось огромное число различных методов. Наиболее используемые из них в психологии:

• Метод главных компонент.
• Метод главных факторов.
• Метод максимального правдоподобия (Д.Лолли).
• Метод минимальных остатков (Г.Харман).
• Альфа-факторный анализ.

Перечисленные методы отличаются по способу поиска решения основного уравнения ФА. Выбор метода требует большого опыта работы. Однако некоторые исследователи используют сразу несколько методов, выделенные же во всех методах факторы считают наиболее устойчивыми.

Все описанные выше модели ФА относятся к эксплораторному (поисковому) ФА. Настоящим переворотом в ФА было изобретение конфирматорного (подтверждающего) анализа – КФА.

Основной принцип КФА: в качестве гипотезы формируется структура ожидаемой матрицы факторных нагрузок (весов), которая затем накладывается на заданную корреляционную матрицу. Гипотеза подвергается статистической проверке, и постепенно исследователь приходит к соответствующей экспериментальным данным матрице нагрузок, не прибегая к вращению факторов.

Однако гипотеза должна основываться на серьёзном анализе природы изучаемых переменных и лежащих в их основе факторов. Часто для этого проводится предварительный эксплораторный ФА. В качестве математического аппарата в данной модели используется моделирование с помощью линейных структурных уравнений.

Данный подход предполагает априорное формулирование гипотез относительно количества латентных и измеряемых переменных, а также их взаимосвязи.

Метод КФА позволяет оценить валидность тестов (конструктную, дискриминантную, конвергентную). Использование множества индикаторов для каждого латентного конструкта даёт возможность представить степень, с которой каждая переменная объясняет латентную переменную. Остаточная дисперсия обусловлена случайными флуктуациями. С помощью параметров измерительной модели определяется внутренняя согласованность теста, по которой можно говорить об уровне надёжности измерения.

Модель латентных классов.

Все модели латентных структур предполагают локальную независимость характеристик. То есть, для данной латентной характеристики наблюдаемые переменные независимы в смысле теории вероятностей.

В основе модели лежит формула Байеса (с учётом экспериментальных данных) их апостериорной плотности распределения. Априорно задаются две латентные характеристики: количество классов (K) и соответствующее им относительное число испытуемых в классе – P(k), а также параметр, позволяющий устанавливать степень вероятности определённого ответа на i -й вопрос при условии, что испытуемый относится к k -му классу – r(k). Априорное задание этих латентных характеристик соответствует гипотезе исследователя, либо задаётся стандартными способами.

Вероятность появления i -го профиля 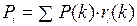. По формуле Байеса вычисляется апостериорная (с учётом реальных профилей ответов на вопросы теста) вероятность принадлежности к классу k при условии, что испытуемый имеет i -паттерн ответов:

.

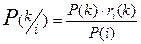Для каждого класса строится наиболее вероятный профиль ответов его представителей.

Данный метод полезен при адаптации существующих новых опросников и их разработке, а также для анализа результатов исследования. (J.Rost, 1988; Т.Савченко, 1995). При адаптации опросников метод латентно-структурного анализа (LSA) позволяет выделить вопросы теста, которые не соответствуют предложенной модели и подлежат замене или переформулированию. Метод LSA используется также для проведения типологизации по множественному критерию.

Дата добавления: 2014-01-20