Цифровые регуляторы

В непрерывных системах широко используются пропорционально-интегрально-дифференциальные (ПИД) регуляторы, которые представляются идеализированным уравнением:

,

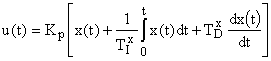где: 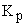— коэффициент усиления пропорционального канала; 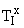— постоянная времени сопрягающего полюса интегрального канала; — постоянная времени сопрягающего полюса дифференциального канала.

Для малых периодов дискретизации 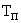уравнение может быть преобразовано в разностное без существенной потери в точности. Непрерывное интегрирование может быть представлено с помощью метода прямоугольников, или метода трапеций.

Метод прямоугольников. Используем этот метод для аппроксимации непрерывного интеграла и запишем ПИД-закон в дискретном виде:

.

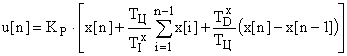В результате получен нерекуррентный (позиционный) алгоритм управления, который требует сохранения всех предыдущих значений сигнала ошибки 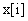, и в котором каждый раз заново вычисляется управляющий сигнал .

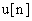Для реализации программ закона регулирования на ЦВМ более удобным является рекуррентный алгоритм. Он характеризуется тем, что для вычисления текущего значения сигнала 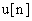используется его предыдущее значение 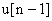и поправочный коэффициент, не требующий существенных вычислительных затрат. Определим его:

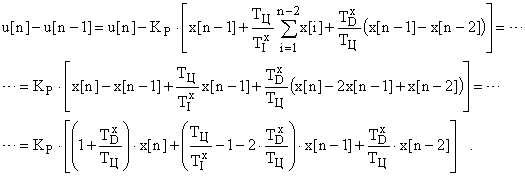
Обозначим в этом выражении:

.

.

.

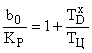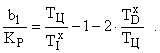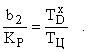Перенесем 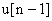в правую часть и получим "скоростной" алгоритм для программной реализации регулятора:

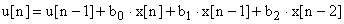
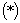
Метод трапеций. Если для аппроксимации непрерывного интеграла использовать метод трапеций, то разностное уравнение будет иметь вид:

.

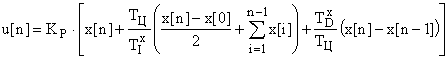Преобразования, аналогичные выше изложенным, при получении рекуррентного соотношения 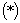, выявляют отличия только для коэффициента :

.

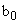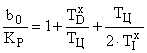Запишем разностное уравнение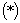 для изображений в 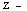домене:

,

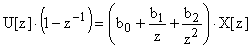и представим его в виде дискретной передаточной функции:

.

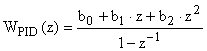Анализ ее коэффициентов показывает, что:

1. Для исключения статической ошибки, передаточная функция должна иметь полюс .
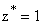2. Если 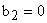, то получим ПИ-регулятор.
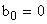3. Если , а 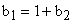, то получим пропорциональнодифференциальный регулятор.

Дата добавления: 2014-01-20