Алгоритмы программ цифровых фильтров

Существует три основных алгоритма программной реализации дискретных передаточных функций (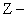передаточных функций):

No алгоритма	Алгоритм	Требуемое быстродействие	Объ¨м памяти
	Непосредственный а) с двумя буферами б) с одним буфером		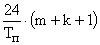9m+9k+12
	Последовательный		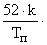20k+10
	Параллельный		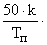19k+8

Дискретную передаточную функцию можно представить в любой из форм:

Алгоритм 1.

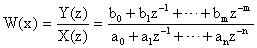— стандартная форма для дискретных передаточных функций.

Алгоритм 2. — разложение 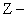передаточных функций на множители

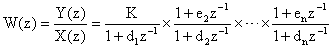
Алгоритм 3. — разложение 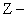передаточных функций на элементарные дроби вида

,

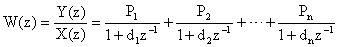где: 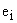— нули z-передаточной функции; 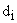— полюса 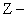передаточной функции; 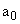— не равно нулю; 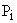— коэффициенты разложения

Этим формам представления z-передаточных функций соответствуют структурные схемы изображенные на рис. 4.

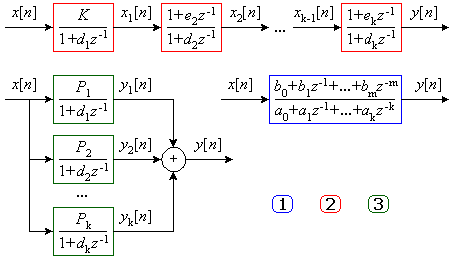
Рис. 4. Варианты построения цифровых фильтров

Разложения по алгоритмам 2 и 3 делают параметры z-передаточных функций независимыми, позволяют контролировать ряд дополнительных фазовых координат: 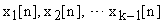; или 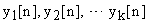— что удобно при отладке систем.

• Последовательная структура алгоритма 2 удобна при синтезе дискретной коррекции.
• Параллельная структура алгоритма 3 удобна для построения цифровых регуляторов.
• Разложение 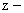передаточных функций на элементарные дроби алгоритма 3 позволяет реализовать 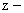передаточных функций на параллельно работающих ЦВМ для повышения быстродействия.

Перечисленные факторы определяют выбор алгоритма программы для ЦВМ.

После разложений, каждый из множителей в форме алгоритма 2 или каждую из элементарных дробей в форме алгоритма 3 следует представить в стандартной форме по алгоритму 1 (с отрицательными степенями оператора z). Переход к разностным уравнениям будет един. 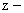передаточную функцию в форме по алгоритму 1 соответствует разностное уравнение вида:

,

по которому и составляется программа. Поскольку текущее значение выходной координаты 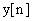рассчитывается по предыдущим значениям 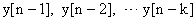— данное разностное уравнение называется рекурсивным.

Изобразим структурную схему цифрового фильтра для этого уравнения (см. рис. 5). Ее можно преобразовать, объединив два буфера (см. рис. 6). Цепочки элементов 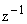в программах будут соответствовать буферам из ячеек памяти, данные в которых сдвигаются на каждом такте дискретизации.

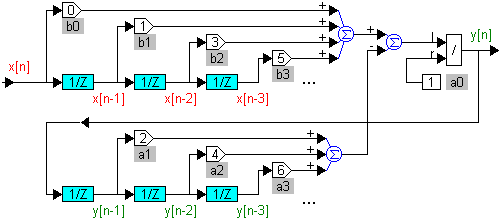
Рис. 5. Структурная схема цифрового регулятора.

Структурной схеме соответствует алгоритм 1. Условие ее физической реализуемости —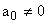

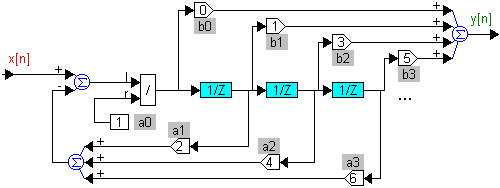
Рис. 6. Преобразованная структурная схема цифрового регулятора.

Если выбран последовательный алгоритм 2 или параллельный алгоритм 3, то структура каждого множителя или элементарной дроби первого порядка (см. рис. 1) будет иметь более простой вид (см. рис. 7).

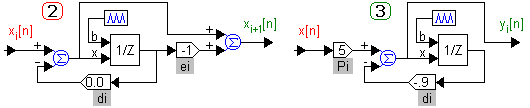
Рис. 7. Схемы цифровых регуляторов по алгоритмам 2 и 3.

Согласно структурной схеме рис. 5, составим процедуру, реализующую дискретную передаточную функцию второго порядка:

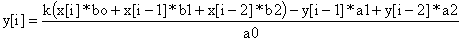
где: 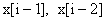и 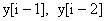— ячейки двух буферов, т.е. регистры задержки — .

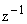По этому уравнению выбираем коэффициенты z-передаточной функции для расчета переходной характеристики и проводится ее построение.

Дата добавления: 2014-01-20