
- Р Р‡.МессенРТвЂВВВВВВВжер
- ВКонтакте
- РћРТвЂВВВВВВВнокласснРСвЂВВВВВВВРєРСвЂВВВВВВВ
- РњРѕР№ Р В Р’В Р РЋРЎв„ўР В Р’В Р РЋРІР‚ВВВВВВВРЎР‚
- LiveJournal
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Система уравнений внутренней баллистики
|
|
|
|
Содержание основной задачи.
Теоретическая внутренняя баллистика рассматривает большое число задач, среди которых выделяют основную задачу, состоящую в установлении соотношений между пиродинамическими элементами и параметрами артиллерийской системы. При этом решают прямые задачи, состоящие в определении пиродинамических элементов, и обратные задачи, состоящие в определении параметров артиллерийской системы.
Решение основной задачи классической внутренней баллистики производится при следующих допущениях:
1. Горение порохового заряда подчиняется геометрическому закону горения.
2. Справедлив линейный закон скорости горения пороха.
3. Состав пороховых газов не изменяется.
4. Теплопередача от пороховых газов к стенкам ствола отсутствует.
5. Продукты горения - пороховые газы и несгоревший порох - распределены равномерно в заснарядном пространстве.
6. Волнообразное движение продуктов горения не рассматривается.
7. Сила сопротивления поступательному движению снаряда, а также разница между скоростью снаряда относительно ствола и баллистическим давлением, с одной стороны, и скоростью снаряда относительно Земли и давлением пороховых газов на дно снаряда, с другой стороны, учитываются с помощью коэффициента фиктивности.
8. Второстепенные работы, затрачиваемые пороховыми газами, пропорциональны основной работе и учитываются с помощью коэффициента фиктивности.
9. Период форсирования не рассматривается, а сила сопротивления врезанию учитывается через начальные условия движения снаряда.
10. Параметр расширения пороховых газов не изменяется.
11. Процесс истечения пороховых газов отсутствует (т. е. прорыв газов между стволом и снарядом).
Схема явления выстрела, отвечающая принятым допущениям, соответствует действительному характеру явления выстрела в классическом орудии, имеющем ствол с закрытым сзади цилиндрическим каналом. Эта схема позволяет с достаточной точностью решить большинство задач, которые выдвигает артиллерийская практика перед внутренней баллистикой.
Таким образом, при решении основной задачи внутренней баллистики явление выстрела делится на три периода: предварительный (пиростатический), первый (пиродинамический), второй (термодинамический), а из всех процессов явления выстрела в явном виде подробно рассматриваются четыре основных процесса: горение пороха, образование пороховых газов, расширение пороховых газов, поступательное движение снаряда.
Под системой уравнений внутренней баллистики принято понимать систему уравнений для наиболее сложного из трех рассматриваемых периодов - первого периода.
Система уравнений при аргументе является наиболее естественной и наглядной. Ею целесообразно пользоваться при проведении исследовании с применением ЭВМ.
Процесс горения пороха описывается уравнением
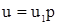 (2.1)
(2.1)
Процесс образования пороховых газов описывается уравнением
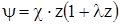 (2.2)
(2.2)
Процесс расширения пороховых газов описывается основным уравнением пиродинамики.
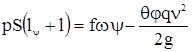 (2.3)
(2.3)
Процесс поступательного движения снаряда описывается уравнением
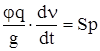 (2.4)
(2.4)
Чтобы система уравнений стала полной, добавим к этим уравнениям еще введенные ранее соотношения между переменными величинами
 (2.5)
(2.5)  (2.6)
(2.6) 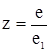 (2.7)
(2.7)
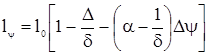 (2.8)
(2.8)
Таким образом, решая эту систему, можно выразить восемь из перечисленных переменных величин в функции от девятой величины t, принятой за аргумент.
Переменные "u" и "е" сами по себе не представляют интереса и могут быть исключены из полученной системы.
Продифференцируем по t уравнение 2.7 и заменим "dе" с помощью уравнения 2.6
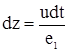
Учитывая выражение 2.1 и вводя величину конечного импульса 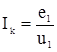 , получим вместо двух уравнений 2.6 и 2.7 одно дифференциальное уравнение
, получим вместо двух уравнений 2.6 и 2.7 одно дифференциальное уравнение
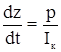 (2.9)
(2.9)
В результате система уравнений внутренней баллистики принимает вид
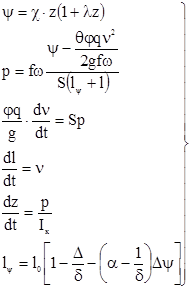 (2.10)
(2.10)
Эта система является замкнутой и допускает единственное решение.
Отсчет времени начинается от момента начала движения снаряда, т. е. допускается, что все процессы в предварительном периоде происходят мгновенно.
При решении системы 2.10 процесс врезания снаряда в нарезы учитывается косвенно с помощью так называемого давления форсирования р0.
Будем считать, что движение снаряда начинается в момент, когда давление пороховых газов в каморе достигает величины давления форсирования р0. При этом сгорит часть пороха, определяемая величинами y0 и z0. На основании формулы пиростатики будем иметь
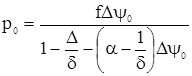
Решая это уравнение относительно y0, найдем
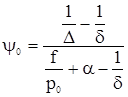 (2.11)
(2.11)
Зная величину y0, можем найти z0 на основании уравнения 2.2
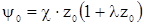 (2.12)
(2.12)
которое является квадратным уравнением относительно z0. Учитывая малость величины z0 по сравнению с единицей, в первом приближении можно пренебречь величиной lz0 и записать
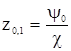 (2.13)
(2.13)
Для определения z0 во втором приближении, подставляем z0,1 в скобку правой части равенства 2.12, в результате чего получим
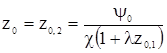
Или после замены z0,1 его выражением 2.13
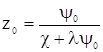 (2.14)
(2.14)
Начальное значение величины ly будет равно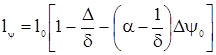 (2.15)
(2.15)
Таким образом, решение системы уравнений 2.10 необходимо вести при следующих начальных условиях:
при t = 0, V = 0, l=0, z = z0
|
|
|
Дата добавления: 2014-01-20; Просмотров: 3189; Нарушение авторских прав?; Мы поможем в написании вашей работы!