
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Наибольшее и наименьшее значение функции
|
|
|
|
Определение. Пусть функция двух переменных  задана на некотором множестве
задана на некотором множестве 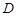 и
и  — некоторая точка этого множества. Точка
— некоторая точка этого множества. Точка 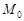 называется точкой глобального или абсолютного максимума (минимума) функции
называется точкой глобального или абсолютного максимума (минимума) функции  , если для всех точек
, если для всех точек 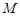 , принадлежащих области
, принадлежащих области 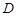 , справедливо неравенство
, справедливо неравенство
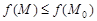 (
( ).
).
Если имеет место строгое неравенство
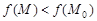 (
(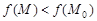 ,
,
то точка 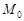 называется точкой строгого глобального или абсолютного максимума (минимума)
называется точкой строгого глобального или абсолютного максимума (минимума)
Такие точки называются точками глобального или абсолютного экстремума, а значение функции в данных точках — глобальным или абсолютным экстремумом. Значение функции в точке глобального максимума называют также наибольшим значением функции на множестве 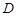 , а в точке глобального минимума — наименьшим значением функции.
, а в точке глобального минимума — наименьшим значением функции.
Как известно, если функция непрерывна на ограниченном замкнутом множестве, то есть на этом множестве найдутся точка, в которой функция принимает наибольшее значение, и точка, в которой функция принимает наименьшее значение. Следовательно, непрерывная на ограниченном замкнутом множестве функция имеет на этом множестве по крайней мере одну точку глобального максимума и одну точку глобального минимума.
Заметим, что, если множество не является ограниченным и замкнутым, то функция может и не иметь на этом множестве наибольшего или наименьшего значения.
Рассмотрим ограниченную замкнутую область, задаваемую системой неравенств
 ,
,  ,
,
где 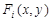 — непрерывные функции. Эта область представляет собой криволинейный многоугольник, сторонами которого являются участки непрерывных кривых
— непрерывные функции. Эта область представляет собой криволинейный многоугольник, сторонами которого являются участки непрерывных кривых  , а вершинами — точки пересечения этих кривых.
, а вершинами — точки пересечения этих кривых.
Для того, чтобы найти наибольшее и наименьшее значения функции в рассматриваемой области, следует вычислить значения локальных экстремумов внутри области, условных экстремумов на каждой из сторон многоугольника при условии  , значения функции в вершинах многоугольника и выбрать из этих значений наибольшее и наименьшее.
, значения функции в вершинах многоугольника и выбрать из этих значений наибольшее и наименьшее.
Заметим, что, если функция дифференцируема в рассматриваемой области, вместо локальных и условных экстремумов можно найти значения функции в стационарных точках внутри области и на ее границах, не проверяя достаточных условий существования экстремума. Действительно, если стационарная точка не является точкой локального или условного экстремума, то она не может быть и точкой глобального экстремума.
Пример 3. Найти наибольшее и наименьшее значения функции  в области
в области 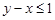 ,
, 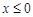 ,
,  .
.
 Данная область является треугольником с вершинами
Данная область является треугольником с вершинами  ,
,  и
и  , стороны которого расположены на прямых
, стороны которого расположены на прямых  ,
, 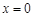 ,
,  (рис. 1).
(рис. 1).
1) Найдем стационарные точки внутри области. Вычислим частные производные функции  и приравняем их нулю
и приравняем их нулю
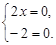
Полученная система не имеет решения. Следовательно, стационарных точек внутри области нет.
Рис. 1
2) Найдем стационарные точки на стороне  . Координаты точек, лежащих на
. Координаты точек, лежащих на  удовлетворяют условиям
удовлетворяют условиям  ,
,  . Тогда рассматриваемая функция принимает вид
. Тогда рассматриваемая функция принимает вид  . Стационарная точка определяется из условия
. Стационарная точка определяется из условия  . Отсюда
. Отсюда 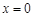 . Вычислим значение функции в найденной точке
. Вычислим значение функции в найденной точке  .
.
3) Рассмотрим точки, лежащие на стороне  . Их координаты удовлетворяют условиям
. Их координаты удовлетворяют условиям 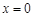 ,
,  . При этом имеем
. При этом имеем 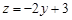 ,
,  , то есть на стороне
, то есть на стороне  стационарных точек нет.
стационарных точек нет.
4) Найдем стационарные точки на стороне  . Здесь
. Здесь 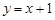 ,
,  ,
,  ,
,  . Из уравнения
. Из уравнения  находим стационарную точку
находим стационарную точку  . Однако она не принадлежит рассматриваемому отрезку.
. Однако она не принадлежит рассматриваемому отрезку.
5) Найдем значения функции в вершинах треугольника
 ,
, 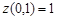 ,
,  .
.
Так как единственная стационарная точка совпала с вершиной треугольника  , выберем наибольшее и наименьшее из этих значений. Итак, функция принимает наибольшее значение
, выберем наибольшее и наименьшее из этих значений. Итак, функция принимает наибольшее значение 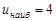 в точке
в точке 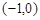 , наименьшее значение
, наименьшее значение  в точке
в точке  .
.
|
|
|
|
Дата добавления: 2014-01-20; Просмотров: 3214; Нарушение авторских прав?; Мы поможем в написании вашей работы!