Лекция 15. Пусть первое слагаемое Х записано в регистрах R0 и R1:

Пример

Пример

Пример

Пример

ПРИМЕР

Пример

Пусть первое слагаемое Х записано в регистрах R0 и R1:

X = 256*(R1) + (R0),

а второе — Y — в регистрах R2 и R3:

Y = 256*(R3) + (R2),

т.е. в регистрах с четными номерами хранятся младшие байты.

Составить фрагмент программы суммирования с записью суммы на место первого слагаемого, т.е. в регистры R1 и R0.

mov	A,	R0	;Взять младший байт первого слагаемого в аккумулятор
add	A,	R2	;Сложить с младшим байтом второго слагаемого
mov	R0,	A	;Запомнить младший байт суммы
mov	A,	R1	;Взять старший байт первого слагаемого в аккумулятор
addc	A,	R3	;Сложить со старшим байтом второго слагаемого;и возможным переносом
mov	R1,	A	;Запомнить старший байт суммы

Этот фрагмент можно оформить в виде подпрограммы:

Add_16:				;Метка или имя подпрограммы
	push	Acc		;Сохранить аккумулятор
	mov	A,	R0	;Взять младший байт первого слагаемого в;аккумулятор
	add	A,	R2	;Сложить с младшим байтом второго слагаемого
	mov	R0,	A	;Запомнить младший байт суммы
	mov	A,	R1	;Взять старший байт первого слагаемого в;аккумулятор
	addc	A,	R3	;Сложить со старшим байтом второго;слагаемого и возможным переносом
	mov	R1,	A	;Запомнить старший байт суммы
	pop	Acc		;Восстановить аккумулятор
	ret			;Возврат из подпрограммы

Составим возможный фрагмент основной программы, использующей подпрограмму Add_16.

Пусть 2-х байтовые числа X и Y находятся в памяти данных по адресам c метками М_х и М_у соответственно. Вычислить с помощью подпрограммы Add_16 сумму этих чисел и результат поместить в память по адресу с меткой Sum.

Память данных

	...
	Старший байт суммы	35h
Sum:	Младший байт суммы	34h
	Y(1)	33h
M_y:	Y(0)	32h
	X(1)	31h
M_x:	X(0)	30h
	...

...
My_Data	SEGMENT	DATA		;
	RSEG	My_Data		;
...
	ORG	30h		;
M_x:	DS			;
M_y:	DS			;
Sum:	DS			;
...
My_Code	SEGMENT	CODE		;
	RSEG	My_Code		;
...
	mov	R0,	M_x	;
	mov	R1,	M_x+1	;
	mov	R2,	M_y	;
	mov	R3,	M_y+1	;
	call	Add_16		;
	mov	Sum,	R0	;
	mov	Sum+1,	R1	;
...
Add_16:				;Метка или имя подпрограммы
	push	Acc		;Сохранить аккумулятор
	mov	A,	R0
	add	A,	R2
	mov	R0,	A
	mov	A,	R1
	addc	A,	R3
	mov	R1,	A
	pop	Acc		;Восстановить аккумулятор
	ret			;Возврат из подпрограммы
	END

Подпрограмму Add_16 можно оформить в виде отдельного модуля, который будет храниться в отдельном файле, например, с именем Add_16.asm, а после трансляции в файле с именем Add_16.obj.

My_Code	SEGMENT	CODE		;
Add_16	PUBLIC			;
	RSEG	My_Code
Add_16:				;Метка или имя подпрограммы
	push	Acc		;Сохранить аккумулятор
	mov	A,	R0
	add	A,	R2
	mov	R0,	A
	mov	A,	R1
	addc	A,	R3
	mov	R1,	A
	pop	Acc		;Восстановить аккумулятор
	ret			;Возврат из подпрограммы
	END

Тогда основная программа примет вид:

...
My_Data	SEGMENT	DATA		;
EXTRN	CODE	(Add_16)		;
	RSEG	My_Data		;
...
	ORG	30h		;
M_x:	DS			;
M_y:	DS			;
Sum:	DS			;
...
My_Code	SEGMENT	CODE		;
	RSEG	My_Code		;
...
	mov	R0,	M_x	;
	mov	R1,	M_x+1	;
	mov	R2,	M_y	;
	mov	R3,	M_y+1	;
	call	Add_16		;
	mov	Sum,	R0	;
	mov	Sum+1	R1	;
...
	END			;

и тоже будет храниться в отдельном файле, например с именем My_Prog_1.asm, а после трансляции в файле с именем My_Prog_1.obj. Для того чтобы редактор связей Link мог собрать эти модули в единую программу, имена этих файлов должны присутствовать в файле проекта.

Поставим задачу сложения двух положительных чисел с форматом 5 байтов. Для ее решения потребуется организовать цикл. Цикл организуем с помощью команды передачи управления:

Декремент регистра и переход, если не нуль	DJNZ Rn, rel	(PC) ¬ (PC) + 2, (Rn) ¬ (Rn) - 1, если (Rn) ≠ 0, то (PC) ¬ (PC) + rel
...
My_Data	SEGMENТ	DATA		;
	RSEG	My_Data		;
...
	ORG	30h		;
M_x:	DS			;5 байтов для первого слагаемого
M_y:	DS			;5 байтов для второго слагаемого
Считая, что запись слагаемых осуществлена в другой части программы, напишем фрагмент сложения первого числа со вторым и с записью суммы на место первого числа.
My_Code	SEGMENT	CODE		;
	RSEG	My_Code		;
...
	mov	R0,	#M_x	;указатель адреса байта первого;числа
	mov	R1,	#M_y	;указатель адреса байта второго;числа
	mov	R3,	#5	;счетчик байтов
	clr	C		;очистка бита переноса
M_add:	mov	A,	@R0	;взять байт первого числа
	addc	A,	@R1	;прибавить байт второго числа
	mov	@R0,	A	;запомнить байт суммы
	inc	R0		;указать на следующий байт;первого числа
	inc	R1		;указать на следующий байт;второго числа
	djnz	R3,	M_add	;подсчет количества;необработанных байтов
...

2. Вычитание.

Пусть уменьшаемое Х записано в регистрах R0 и R1:

X = 256*(R1) + (R0),

а вычитаемое — Y — в регистрах R2 и R3:

Y = 256*(R3) + (R2),

т.е. в регистрах с четными номерами хранятся младшие байты.

Составить фрагмент программы вычитания с записью разности на место уменьшаемого, т.е. в регистры R1 и R0.

clr	C		;Очистить бит заëма (переноса)
mov	A,	R0	;Взять младший байт уменьшаемого в аккумулятор
subb	A,	R2	;Вычесть младший байт вычитаемого
mov	R0,	A	;Запомнить младший байт разности
mov	A,	R1	;Взять старший байт уменьшаемого в аккумулятор
subb	A,	R3	;Вычесть старший байт уменьшаемого
mov	R1,	A	;Запомнить старший байт разности

3. Умножение

4.2 Умножение на целую степень двойки

Умножение двоичного числа, состоящего из нескольких байтов, на целую степень двойки осуществляется при помощи сдвига всех байтов этого числа влево. Для умножения на 2 нужен сдвиг влево на 1 разряд, для умножения на 4 — на 2 разряда и т.д.

00000001₂ = 1₁₀,

¬

00000010₂ = 2₁₀,

¬

00000100₂ = 4₁₀.

Вспомним, какие команды сдвигов влево имеются в нашем распоряжении.

Сдвиг аккумулятора влево циклический	RL A	(An+1) ¬ (An), n=0÷6, (A0) ¬ (A7)
Сдвиг аккумулятора влево через перенос	RLC A	(An+1) ¬ (An), n=0÷6 (A0) ¬ (C), (C) ¬ (A7)

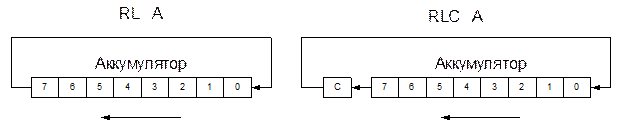
Видим, что для сдвига байта его нужно предварительно поместить в аккумулятор.

Пусть число Х записано в регистрах R0 и R1: X = 256*(R1) + (R0).

Умножить число на 2 и записать на прежнее место.

clr C;Очистить флаг переноса

mov a, R0;Взять мл. байт

rlc a;Умножить на 2

mov R0, a;Положить на место

mov a,R1;Взять ст. байт

rlc a;Умножить на 2

mov R1, a;Положить на место

Умножить число на 8 и записать на прежнее место.

mov R2, #3;Счетчик сдвигов

Repeat: clr C;Очистить флаг переноса

mov a, R0;Взять мл. байт

rlc a;Умножить на 2

mov R0, a;Положить на место

mov a, R1;Взять ст. байт

rlc a;Умножить на 2

mov R1, a;Положить на место

djnz R2, Repeat;Подсчет числа сдвигов

4.2 Перемножение произвольных положительных чисел

При перемножении чисел, каждое из которых представлено двумя байтами, произведение может занять 4 байта.

Вспомним команду умножения.

Умножение аккумулятора на регистр В

MUL AB

(B)(A) ¬ (A)*(В)

Если результат произведения больше чем 0FFh (255), то устанавливается флаг переполнения OV, в противном случае он сбрасывается. Флаг переноса С всегда сбрасывается.

Обозначим:

X = 2⁸ *Х(1) + Х(0) = 256*X(1) +X(0) — первое двухбайтовое число,

Y = 2⁸ *Y(1) + Y(0) = 256*Y(1) +Y(0) — второе двухбайтовое число,

где

Х(1), Y(1) — старшие байты, Х(0), Y(0) — младшие байты чисел;

Умножение проведем «столбиком»

256*X(1) + X(0)

256*Y(1) + Y(0)

256*X(1)*Y(0) + X(0)*Y(0)

65536*X(1)Y(1) + 256*Y(1)*X(0)

65536*X(1)*Y(1) + 256*[X(1)*Y(0) + X(0)*Y(1)] + X(0)*Y(0)

Два байта

Два байта

Два байта

Два байта

Положим для определенности, что байт Х(0) находится в R0 и т.д.

X(0) à R0, X(1) à R1, Y(0) à R2, Y(1) à R3.

Результат умножения поместим в регистры R4, R5, R6 и R7. Причем старшие байты находятся в регистрах с большими номерами.

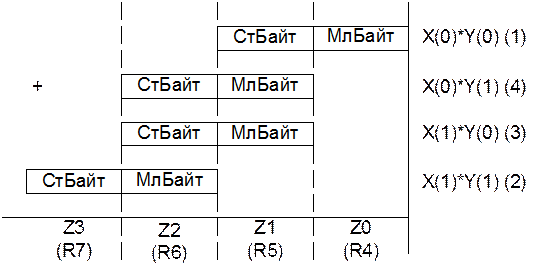
Обозначим: Z0 текущее содержимое регистра R4, т.е. Z0à R4, Z1 à R5,
Z2 à R6, Z3 à R7,

Z0 = МБ[X0·Y0] (МБ — младший байт произведения),

Z1 =СБ[X0·Y0]+МБ[X1·Y0]+МБ[X0·Y1] (СБ — старший байт произведения),

Z2 =СБ[X1·Y0]+СБ[X0·Y1]+МБ[X1·Y1],

Z3=СБ[X1·Y1].

Видим, что для получения результата надо выполнить 4 умножения и 4 сложения. Умножения будем проводить в следующем порядке:

1. X0·Y0

2. X1·Y1

3. X1·Y0

4. X0·Y1

Фрагмент программы умножения двухбайтовых положительных чисел имеет вид:

mov A, R0;забрали X0

mov B, R2;забрали Y0

mul AB;(A) = МБ[X0·Y0]; (B) = СБ[X0·Y0]

mov R4, A;получили Z0 и положили на место

mov R5, B;получили заготовку Z1¢

mov A, R1;забрали X1

mov B, R3;забрали Y1

mul AB;(A) = МБ[X1·Y1]; (B) = СБ[X1,Y1]

mov R6, A;получили заготовку Z2¢

mov R7, B;получили заготовку Z3’

mov A, R1;забираем X1 в А

mov B, R2;забираем Y0

mul AB;(A) = МБ[X1·Y0]; (B) = СБ[X1,Y0]

add A, R5;складываем

mov R5, A;получаем заготовку Z1’’

mov A, R6;забираем R6

addc A, B;(А) = СБ[X1·Y0]+МБ[X1,Y0] => Z2’’

jnc nc1;перейти, если нет переноса

inc R7;учли возможный перенос

nc1: mov R6, A;Z2’’

mov A, R0;забираем X0 в A

mov B, R3;забираем Y1

mul AB;(A) = МБ[X0·Y1]; (B) = СБ[X0,Y1]

add A, R5;

mov R5, A;Z1 на месте

mov A, R6;Z2’’ в A

addc A, B;в A находится Z2

jnc nc2;перейти если нет переноса

inc R7;учет переноса в Z3. Z3 на месте

nc2: mov R6, A;получили Z2 и положили на место

4. Деление

4.2 Деление на целую степень двойки

Деление двоичного числа, состоящего из нескольких байтов, на целую степень двойки осуществляется при помощи сдвига всех байтов этого числа вправо. Для деления на 2 нужен сдвиг вправо на 1 разряд, для деления на 4 — на 2 разряда и т.д.

00001000₂ = 8₁₀,

®

00000100₂ = 4₁₀,

®

00000010₂ = 2₁₀.

Вспомним, какие команды сдвигов вправо имеются в нашем распоряжении.

Сдвиг аккумулятора вправо циклический	RR A	(An) ¬ (An+1), n=0÷6, (A7) ¬ (A0)
Сдвиг аккумулятора вправо через перенос	RRC A	(An) ¬ (An+1), n=0÷6 (A7) ¬ (C), (C) ¬ (A0)

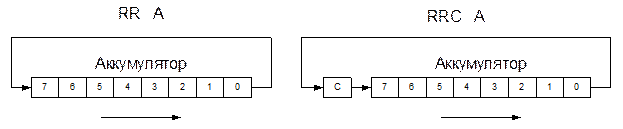
Видим, что для сдвига байта его нужно предварительно поместить в аккумулятор.

Пусть число Х записано в регистрах R0 и R1: X = 256*(R1) + (R0).

Разделить число на 2 и записать на прежнее место.

clr C;Очистить флаг переноса

mov a, R1;Взять ст. байт

rrc a;Разделить на 2

mov R1, a;Положить на место

mov a,R0;Взять мл. байт

rrc a;Разделить на 2

mov R0, a;Положить на место

Разделить число на 8 и записать на прежнее место.

mov R2, #3;Счетчик сдвигов

Repeat: clr C;Очистить флаг переноса

mov a, R1;Взять ст. байт

rrc a;Разделить на 2

mov R1, a;Положить на место

mov a, R0;Взять мл. байт

rrc a;Разделить на 2

mov R0, a;Положить на место

djnz R2, Repeat;Подсчет числа сдвигов

4.2 Деление произвольных чисел

Затруднено из-за отсутствия конечных формул для вычисления частного и остатка. В качестве примера рассмотрим деление двухбайтового числа Х = 256*Х(1) + Х(0) на однобайтовое Y = Y(0).

.

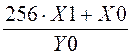Операция целочисленного деления заключается в приведении неправильной дроби к правильной, при этом целая часть результата является частным, а числитель дробной части — остатком: .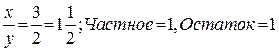

Обозначим частное — Q, остаток — R. Тогда задача целочисленного деления сводится к нахождению двух неотрицательных целых чисел, удовлетворяющих уравнению и неравенству

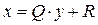
R < y

Это уравнение решается подбором частного, т. е. методом проб и ошибок. Например, это можно делать многократным вычитанием делителя из делимого до тех пор, пока остаток не будет меньше делителя. Тогда частное равно количеству операций вычитания. Недостаток — большое время выполнения.

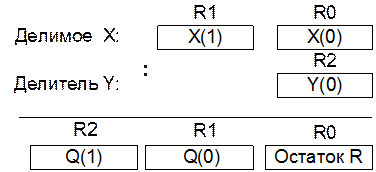
Выполнить самостоятельно.

Колебательные и волновые процессы

Гармонические колебания. Дифференциальное уравнение колебаний. Маятники. Сложение одинаково направленных колебаний (метод векторных диаграмм). Сложение двух взаимно перпендикулярных колебаний.

Источник: Детлаф Яворский 2002г. Глава 27. С. 358-370

Колебания: определение, классификация.

Колебательным называют процесс, при котором какая-либо физическая величина изменяется не монотонно, а претерпевает переменные увеличения и уменьшения. Колебаниями называются процессы, при которых какая-либо физическая величина принимает многократно, через равные (или почти равные) последовательные промежутки времени, одни и те же или приблизительно одни и те же значения.

Простейшим и наиболее важным типом периодических колебаний является гармоническое колебание, при котором изменяющиеся во времени физические величины описываются функциями косинуса или синуса.

Система (или материальная точка), совершающая периодическое колебание около положения устойчивого равновесия, называется осциллятором (от латинского слова oscillo – качаюсь).

Свободные (собственные) колебания, вынужденные колебания, а также параметрические и автоколебания.

Собственные колебания происходят в изолированной системе после внешнего однократного возмущения.

Затухающие и вынужденные колебания.

Примером может служить раскачивание установленного на упругой опоре двигателя при вращении его вала (особенно если он не сбалансирован).

Параметрические колебания отличаются от вынужденных родом внешнего воздействия.

Автоколебания – периодические движения, которые возникают в системе в отсутствие внешнего периодического воздействия.

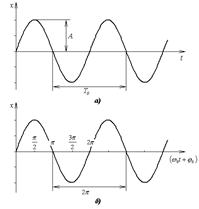
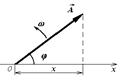
рис.3

Для наглядного сложения одинаково направленных колебаний удобно использовать метод векторных диаграмм. Каждому гармоническому колебанию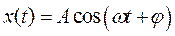можно поставить в соответствие вектор, вращающийся в плоскости xy против часовой стрелки. Длина этого вектора будет равна амплитуде колебаний, угловая скорость вращения вектора – циклической частоте колебания, а начальный угол – начальной фазе колебания.

Дата добавления: 2014-01-20