Андрогенные гормоны

Биения

Сложение колебаний. Параллельные колебания

Если тело одновременно участвует в двух колебаниях вдоль оси X:

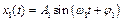и ,

то его координата x определяется выражением:

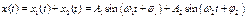. (70)

Согласно методу векторных диаграмм

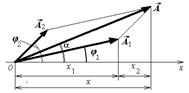
рис. 12

.

.

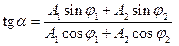
Тогда .Обозначим и, следовательно, .

Стоит отметить, что колебание 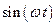происходит с частотой близкой к 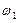и .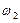

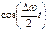изменяется гораздо медленнее, чем 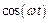, Это дает возможность рассматривать результат сложения колебаний как гармоническое колебание с частотой ω, амплитуда которого медленно изменяется со временем. Такой колебательный процесс носит название биений. Период биений .

рис 13

Перпендикулярные колебания

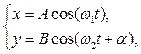Пусть w₁=w₂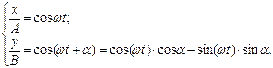

Или

Получившееся уравнениезадает эллипс, вписанный в прямоугольник размером 2 А´ 2 В и повернутый относительно осей координат на некоторый угол (рис. 14).

рис. 14

При некоторых значениях фазового сдвига α уравнение принимает особенно простой вид: а) при α = π k (k=0, ±1, ±2 и т. д.) эллипс вырождается в отрезок прямой;

б) при α = (2 k +1)π/2 (k =0, ±1, ±2 и т. д.) оси эллипса совпадают с осями координат.

Если же периоды колебаний по х и у не соизмеримы, траектория колеблющейся точки будет постепенно заполнять весь прямоугольник.

Если отношение частот в выражается рациональным числом: ω₁/ω₂= m/n, где m, n – целые числа (в этом случае говорят, что частоты ω₁ и ω₂ соизмеримы), траектория движения точки будет представлять собой замкнутую кривую, так как через определенный промежуток времени (равный общему периоду колебаний, который определяется как наименьшее общее кратное периодов колебаний по х и по у) будут повторяться значения обеих координат. Эту кривую (их общее название – фигуры Лиссажу) мы можем наблюдать, например, на экране электронного осциллографа, если на две пары его пластин подать сигналы с соизмеримыми частотами. По форме этой фигуры легко определить отношение частот колебаний по осям х и у: оно равно отношению числа касаний кривой Лиссажу с вертикальными и горизонтальными сторонами описанного прямоугольника соответственно. Так, на рис. 15 первая кривая Лиссажу соответствует ω₁/ω₂=3/1, вторая – ω₁/ω₂=1/2. Обратите внимание, что если кривая Лиссажу не замкнута (как на рис. 15,а), то при подсчете точек касания ее начало и конец учитываются с коэффициентом 1/2.

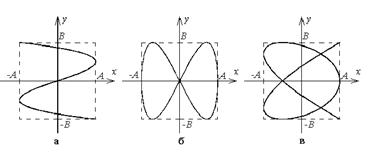рис.15

Андрогенные гормоны мало активны при приеме внутрь, так как они легко разрушаются ферментами печени, поэтому их применяют только в виде инъекций. Кроме того, андрогены быстро выделяются из организма почками. В связи с этим, для пролонгирования их действия, получают сложные эфиры, например, пропионаты. Андрогенные гормоны нецелесообразно применять как анаболики, так как одновременно проявляется высокая андрогенная активность. В результате химической модификации молекулы андрогенного гормона – тестостерона, был создан ряд лекарственных веществ с высокой анаболической активностью и гораздо меньшей андрогенной активностью.

К ним относятся производные тестостерона (А) и 19-нор тестостерона (В).

Дата добавления: 2014-01-20