Спектр одиночного сигнала

Для нахождения спектра воспользуемся комплексной формой ряда Фурье, предположив, что сигнал периодический:

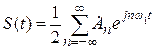; (1)

комплексная амплитуда будет

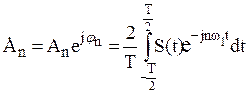. (2)

Как и прежде 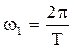. Сделаем предельный переход от периодического к одиночному сигналу. Если T → ¥, то nw₁ → w, то есть будет непрерывной частотой. Часть выражения (2)теперь можно записать так:

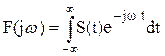, (3)

которая называется спектральной плотностью сигнала. Чтобы понять ее смысл, обратимся к ряду Фурье (1). Его можно записать так:

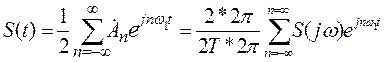. (4)

При предельном переходе 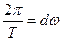, сумма переходит в интеграл, и сигнал будет равен

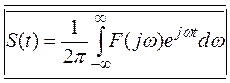. (5)

Поскольку сигнал выражается в вольтах, в правой части (5) также должны бать вольты. Таким образом, F(jw) имеет размерность вольты деленные на рад в сек. (часто В/Гц). отсюда и название данной величины «спектральная плотность». e^jwt – гармонический множитель в комплексной форме. Из (5) можно сделать вывод о том, что сигнал может быть записан в виде суммы бесконечного количества гармонических сигналов с бесконечно малыми комплексными амплитудами

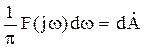. (6)

Спектральная плотность характеризует распределение этих амплитуд по частоте.

В этом суть спектрального представления одиночных сигналов. Выражения (3) и (5) представляют пару интегрального преобразования Фурье, прямое и обратное.

Обратим внимание на то, что модуль и фаза одинаковые по значимости характеристики сигнала, ибо отсутствие любой из них делает невозможным его представление во времени.

Дата добавления: 2014-01-20