Свойства спектральной плотности

а) В отличии от периодических сигналов частотная характеристика одиночного сигнала непрерывная функция частоты. Это означает, что в сигнале есть теоретически все частоты.

б) Модуль спектральной плотности F(w) – функция чётная, а фаза j(w) нечетная функция частоты. На рис 2, 3 показан качественно вид этих функций для гипотетического одиночного сигнала.

F(w)

0 w

Рис.2 Характеристика модуля спектральной плотности

j(w)

0 w

Рис.3 Характеристика фазы спектральной плотности

в) Для вычисления спектра следует руководствоваться следующим:

, (7)

,

.

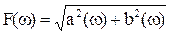г) Интегрирование, посредством которого вычисляется спектр, линейная операция и здесь применим принцип суперпозиции. Есть сигнал состоящий из суммы двух. Спектр суммы равен сумме спектров:

S(t) = S₁(t) + S₂(t),

F(jw) = F₁(jw) + F₂(jw). (8)

д) Допустим, сигнал сдвинут по времени S₁(t - t₁) и нужно определить его спектр по исходному S(t). Здесь (t – t₀) – сдвиг во времени на t₀. Если известно S(t) ® F(jw), то S₁(t) ® . Таким образом, множителем 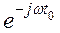в спектральной плотности отражается временной сдвиг. На рис. 4 показан сдвинутый сигнал.

S(t) S(t-t₁))

t₀ t t

Рис.4 Сдвиг сигнала во времени

е) Если исходный сигнал подвергается дифференцированию или интегрированию, соответствующим образом меняется его спектр

, ;

, .

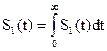Свойства спектра позволят упростить его нахождение при задании конкретного вида сигнала.

Определим спектр простейшего сигнала в виде единичного импульса заданной длительности (рис. 5).

U(t)

1

t t

Рис. 4 Импульсный сигнал

Согласно (3) имеем:

. (9)

По известным в тригонометрии формулам получим выражение для модуля и фазы спектральной плотности:

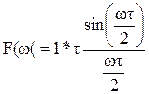, (10)

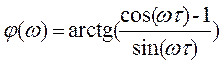. (11)

На рис.5 показано поведение модуля спектральной плотности при различных длительностях импульса.

F(w)

1*t₁

1*t t₁ > t > t₂

1*t₂

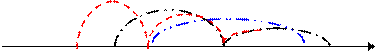w

Рис. 5 спектральная плотность прямоугольного импульса

Теперь мы можем сделать важный для практике вывод. Ширина спектра Δw, хотя бы в пределах главного лепестка зависит от длительности сигнала. Чем короче сигнал тем, шире его спектр и наоборот. Это остается справедливым и для периодических сигналов, у которых так же существует длительность. Эта закономерность получила название принципа неопределенности, Δw*τ=const.

Дата добавления: 2014-01-20