Энергия одиночного сигнала

Она характеризует как амплитуду сигнала, так и время его существования. Вычислить ее через временную функцию можно так:

. (12)

Можно определить эту энергию и по спектру. Докажем это с помощью интегрального преобразования Фурье. Известно, что

,

тогда комплексно сопряженная спектральная плотность будет

. (13)

найдем интеграл от произведения, выразив комплексно сопряженную плотность через функцию сигнала:

В итоге получим известное выражение для энергии. Таким образом

. (14)

Эта формула получила название равенство Парсеваля для одиночного сигнала. Уместно считать, что F²(w) характеризует распределение по частоте энергии сигнала; она имеет следующую размерность:

.

4. Практическая ширина спектра одиночного сигнала

Теоретически бесконечные спектры сигналов необходимо ограничить во многих практических задачах, так как все устройства канала имеют ограниченную полосу пропускания. Естественно встает вопрос о согласованности с ними сигнала. Наиболее объективно ограничение выполнить на основе энергетического критерия. Известное равенство Парсеваля (14) дает полную энергию сигнала в полосе частот от 0 до µ.

Если задать процент от полной энергии сигнала W¢, то ему будет соответствовать определенная граничная частота w_гр и

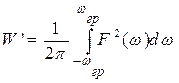. (15)

Таким образом, имея зависимость энергии от верхней частоты можно найти граничную частоту.

5. Вейвлеты

Известно, что для представления сигналов используются ортогональные ряды, 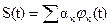, в частности ряд Фурье в различных модификациях. Обратим внимание на базисные функции. Гармонические функции sin(nw₁t) и cos(nw₁t) сосредоточены по спектру и распределены (бесконечны) по времени. Если в качестве базисных принять дельта –функции =δ(t-kΔt), у них другая особенность, сосредоточенность во времени и распределенность по спектру. Таким образом, имеется большой выбор базисных функций и в частности таких, которые сосредоточены как по времени, так и по частоте.

Зачем нужно такое представление?

Допустим, сигнал представлен чередованием двух частот f1 м f2, рис. 5. Такой сигнал является нестационарным, так как его свойства меняются во времени, и его спектр состоит из двух составляющих.

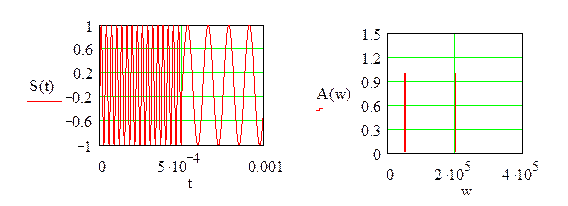
а) б)

Рис. 5. Нестационарный сигнал а) и его спектр б).

Спектральные характеристики не отражают изменение во времени. Правда есть выход и при применении преобразовании Фурье. Существует оконное (кратковременное) преобразование Фурье. Его суть проста: сигнал разбивают на временные окна и в них находят спектр. Получают частотно-временное представление. Окна сдвинуты относительно друг друга га время b, вводят оконную функцию r(t-b) на которую умножают исходную. Если окно прямоугольное, r(t-b)=1 в пределах окна и 0 за пределами. В каждом окне производится свое преобразование,

.

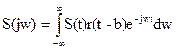В итоге получается набор спектрограмм в каждом окне, который можно показать в формате 3-D с координатами «время частота».

Такой подход имеет принципиальный недостаток. Чем меньше временное окно, тем точнее отражается сигнал во времени, но тем шире его спектр и хуже разрешение по спектру. Нельзя одновременно получить высокое разрешение по времени и по спектру (принцип неопределенности Гейзенберга). В основе используется по-прежнему синусоида.

Однако, было предложено другое решение. Введем функцию, - это материнский вейвлет.

Через материнский вейвлет формируются базисные функции . Множитель 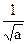- масштабирующий.

Параметр «a» определяет длительность вейвлета, временной масштаб, чем больше, тем шире вейвлет и наоборот. Понятия «шире», «уже» связано с частотой, поэтому временной масштаб «a» и частотный параметр.

Параметр «b» определяет сдвиг вейвлета по времени. Кстати, слово «вейвлет» в переводе означает «короткая волна». В представлении Фурье у базисных функций был один параметр, частота, здесь два – «a» и «b».

Рассмотрим популярный в непрерывном преобразовании вейвлет «мексиканская шляпа», , и ряд функций на его основе:

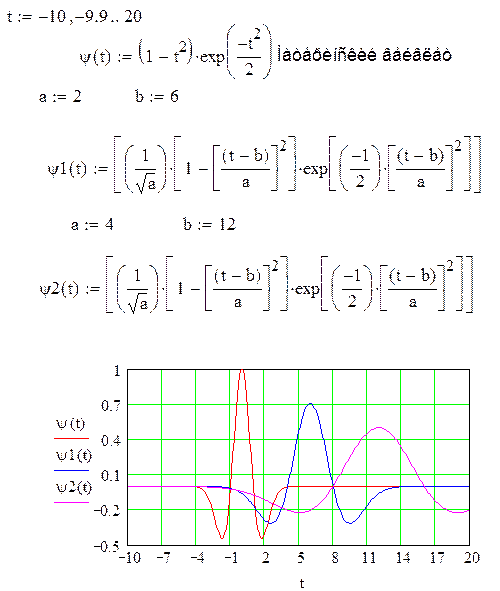
Рис. 6. Базисные функции.

Различная длительность вейвлетов рис. 6 обеспечивает и различные их спектры, рис.7.

Рис. 7 Спектры вейвлетов

Если ввести эффективную длительность вейвлета Δτэ и эффективную полосу частот Δwэ они связаны принципом неопределенности: больше одно меньше другое, рис.8.

Рис. 8. Принцип неопределенности для вейвлетов.

В некотором смысле вейвлет можно уподобить фильтру с полосой Δwэ; его отсутствие в представлении сигнала означает отсутствие части спектра. Существует множество вейвлетов и есть выбор для решения поставленной задачи. Однако все эти функции должны обладать следующими признаками.

1. - энергия вейвлета ограничена.

2. Локализация функции по времени и по частоте.

3. , постоянная составляющая равна нулю. Как следствие спектр равен нулю при w=0. При различных «а» это полосовой фильтр или набор таких фильтров.

4. Автомодальность (самоподобие). Ψ_ab(t) имеет то же количество всплесков, что и материнский вейвлет.

Приведем примеры некоторых популярных вейвлетов.

Непрерывные вейвлеты:

а. «мексиканская шляпа» ,

б. гауссовский певого порядка

Дискретный вейвлет Харра.

Комплексный вейвлет Марле.

.

Таким образом, в самом вейвлете заложены функции окна.

Сигнал представляется совокупностью вейвлетов – коротких волн, созданных на базе материнского вейвлета. Эта совокупность разная в разных частях времени и корректируется множителями. Это и есть вейвлет – анализ сигналов.

Число используемых при разложении вейвлетов – уровень декомпозиции сигнала. Сам сигнал – нулевой уровень декомпозиции. Чем ниже уровень декомпозиции, тем ниже точность, но выше компрессия и появляется возможность исключить шумы. Появляется возможность вейвлет – обработки.

Непрерывное прямое вейвлет – преобразование (НВП, СWТ). Это функция двух аргументов а и b:

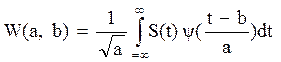, (16)

это вейвлет-спектр. Его визуализация – поверхность в трехмерном пространстве.

Непрерывное обратное вейвлет преобразование (ОНВП) это реконструкция сигнала:

, (17)

где С_ψ – нормирующий коэффициент, .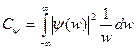

Полное достоинство этого преобразования реализуется при дискретной форме.

Дата добавления: 2014-01-20