Изменение скорости и ускорения

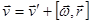
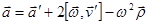, - - осестремительное ускорение, нормальное!

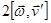- кориол и сово ускорение, тангенциальное.

Дифференцирование и интегрирование

Определение:

производная функции f(x) по x: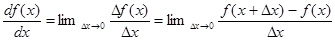

Смысл –угловой коэффициент касательной к f(x) в т. x

Вектор мгновенной скорости и производная:

= =

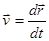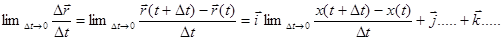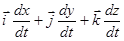= В итоге: три производные от координат!

Определенный интеграл от f(x) в пределах от a до b есть предел интегральной суммы при разбиении промежутка [ ab ] на малые промежутки 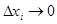, т. е.

Имеет смысл площади под f(x) на [ ab ].

Рис. 2-10

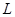Работа силы на траектории между точками 1 и 2 равна сумме работ на элементарных отрезках:

- криволинейный интеграл по .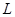

Конец Напоминания.

Проблема движения планет

Воспользуемся полученной информацией для рассмотрения проблемы движения планет Солнечной системы.

РИС. 3-11

Радиус орбиты движения Земли (T) вокруг Солнца (S) 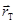»150000000 км.

Если пренебречь взаимодействием между планетами,

задача сводится к проблеме движения материальной точки в поле центральных сил.

Введем понятие секториальной скорости.

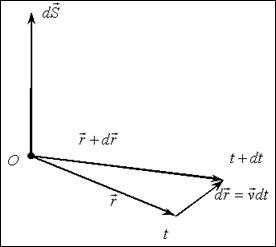Пусть в момент времени t положение точки определяется радиусом-вектором 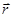, через промежуток времени 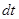- радиусом-вектором .

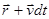РИС. 3-12

Величине 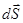придается векторный смысл, чтобы зафиксировать направление движения. Площадь, ометаемая радиусом-вектором точки, движущейся вокруг силового центра О, за время : .

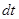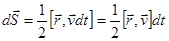Скорость изменения площади, ометаемой радиусом-вектором (секториальная скорость): .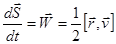

По определению момента количества движения .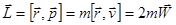

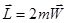- в случае движения материальной точки в центральном поле ее момент количества движения пропорционален ее секториальной скорости.

Два следствия

1) Постоянство вектора – это постоянство не только его абсолютного значения (модуля), но и его направления. Значит, плоскость, перпендикулярная 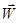, занимает постоянное положение в пространстве; именно в этой плоскости лежат вектора 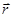и . Следовательно, траектория движения материальной точки в поле центральных сил – это плоская кривая.

1-ый закон Кеплера (1609 год)

В невозмущенном движении, т.е. в задаче двух тел, орбита движущейся точки есть плоская кривая второго порядка, в одном из фокусов которой находится центр силы притяжения.

Планеты движутся вокруг Солнца по эллипсам, в одном из фокусов которых находится Солнце.

2) Из постоянства модуля вектора 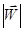следует, что в равные времена радиус-вектор материальной точки, движущейся в поле центральных сил, ометает равные площади.

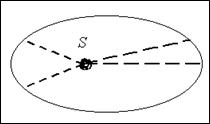
РИС. 3-13

2-ой закон Кеплера (1609 год)

В невозмущенном движении площадь, описываемая радиусом-вектором точки, движущейся в поле центральных сил, изменяется пропорционально времени.

Радиус-вектор планеты за равные промежутки времени описывает равные площади.

Оба эти закона Кеплера были в свое время получены в результате обработки экспериментальных данных Тихо Браге (1546-1601) и привели впоследствии Ньютона к установлению закона всемирного тяготения: 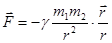- всегда притяжение – единственная сила, управляющая движением астрономических тел.

3-ий закон Кеплера (1619 год).

Формулировка Кеплера:

квадраты времен обращений планет относятся как кубы больших осей эллиптических орбит, по которым они движутся вокруг Солнца: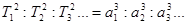

Справедливость 3-го закона Кеплера можно доказать, если считать орбиты планет круговыми. Это предположение не слишком грубое, так как эксцентриситет орбит планет невелик: для орбиты Земли 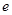»0.017, для орбиты Меркурия 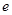»0.205.

Дата добавления: 2014-01-20