ЛЕКЦИЯ 3. Числовые характеристики случайных величин

Числовые характеристики случайных величин

Ключевые термины

Переутомление – невротическое состояние, возникающее при суммировании остаточных явлений предыдущего утомления с на­лич­ным при недостаточном или нерациональном отдыхе (плохой или неполноценный сон), а так­же при чрезмерной рабочей нагрузке.

Работоспособность – способность человека выполнять определенную работу в те­че­ние длительного времени без снижения ее качества и про­из­во­ди­тель­нос­ти.

Стресс – психическое и фи­зи­оло­ги­чес­кое состояние, которое возникает в от­вет на разнообразные экстремальные воздействия. Стресс вызывается ситуацией опасности, возрастания ответственности, необходимостью быстро принять важное решение, большими умственными и во­ле­вы­ми нагрузками.

Усталость – субъективное состояние индивидуума, для которого характерно психическое переживание, связанное с утом­ле­ни­ем. Степень усталости большей частью соответствует степени действительного снижения работоспособности, что в свою очередь связано с ко­ли­чеством и ка­чеством проделанной работы.

Утомление – объективное состояние организма, при котором в ре­зуль­та­те длительной напряженной работы происходит временное снижение работоспособности и ухуд­ше­ние функционального состояния.

Контрольные вопросы

1. Ка­кие факторы влияют на состояние психофизиологического здоровья студента?

2. Ка­ки­ми наиболее значимыми признаками характеризуются усталость, утомление и переутомление? Укажите их причину и методы профилактики.

3. Ка­кое влияние на работоспособность оказывает периодичность ритмических процессов организма?

4. Пе­ре­чис­ли­те общие закономерности изменения работоспособности студентов в про­цес­се обучения:

а) в те­че­ние рабочего дня;

б) в те­че­ние учебной недели;

в) по семестрам и в це­лом за учебный год.

8. Ка­кие особенности физического и пси­хи­чес­ко­го состояния наблюдаются у сту­ден­тов в пе­ри­од экзаменационной сессии?

9. Пе­ре­чис­ли­те средства физической культуры в ре­гу­ли­ро­ва­нии психоэмоционального и функцио­наль­но­го состояния студентов в эк­за­ме­на­ци­он­ный период.

10. Ка­ким образом используются «малые формы» физической культуры в ре­жи­ме учебного труда студентов?

11. Ка­кой режим двигательной активности необходим студентам в про­цес­се учебной деятельности?

Начальные моменты распределения случайной величины. Для случайных величин мы ввели следующие формы закона распределения:

Дискретная случайная величина	Непрерывная случайная величина
1) Функция распределения.	1) Функция распределения.
2) Ряд распределения или многоугольник распределения.	2) Плотность вероятности (кривая плотности вероятности).

Закон распределения является некоторой функцией и даёт исчерпывающую характеристику случайной величины. Однако, установление закона распределения случайной величины часто обременительно, а иногда сопряжено с такими трудностями, что выполнить его становится просто невозможно. Поэтому часто для описания случайных величин применяются некоторые «неполные» характеристики, дающие описание случайной величины, как бы «в общих чертах». Такими характеристиками являются, например, среднее значение случайной величины, около которого группируются её конкретные значения; числовая характеристика, описывающая «разбросанность», или как говорят, рассеивание случайной величины около её среднего значения; а так же некоторые другие характеристики. Такие характеристики, выражающие в компактной числовой форме основные, наиболее существенные особенности распределения случайной величины, носят название числовых характеристик случайной величины. В качестве числовых характеристик случайной величины используются так называемые моменты распределения. Название «моменты» происходит от механической интерпретации этих величин. Начнём с определения моментов для дискретных случайных величин.

Определение 4.1. Пусть 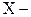некоторая дискретная случайная величина, принимающая возможные значения 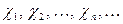с соответствующими вероятностями 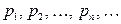. Начальным моментом распределения 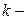го порядка случайной величины 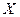называется (числовая) величина, определяемая формулой

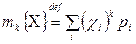. (4.1)

В (4.1) степень мы будем дальше записывать без скобок. В общем случае в правой части (4.1) стоит числовой ряд 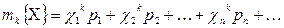, который предполагается абсолютно сходящимся. Вспоминая определение действительного числового векторного (арифметического) пространства, можно записать 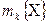в виде скалярного произведения, вводя бесконечные векторы-столбцы вида

, .

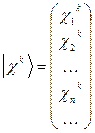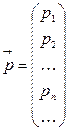
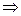
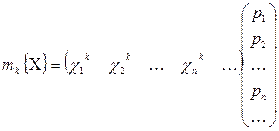Аналогично, для непрерывной случайной величины имеем.

Определение 4.2. Пусть 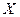– некоторая непрерывная случайная величина Начальным моментом распределения 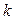-го порядка случайной величины 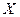называется числовая величина, определяемая формулой

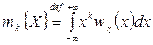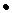. (4.2)

В (4.2) интеграл предполагается абсолютно сходящимся, то есть

.

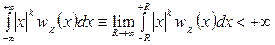Отметим, что моменты распределения существуют не для всяких случайных величин.

Среднее значение (математическое ожидание) случайной величины. Среднее значение или математическое ожидание случайной величины есть числовая характеристика, указывающая некоторое «ориентировочное» её значение, вокруг которого группируются все возможные значения этой случайной величины.

Определение 4.3. Средним значением или математическим ожиданием случайной величины 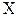(непрерывной или дискретной) называется её начальный момент распределения первого порядка.

Обозначив среднее значение случайной величины 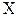, как это принято, символом 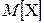, получаем:

для дискретной случайной величины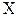

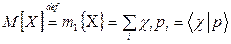; (4.3)

для непрерывной случайной величины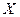

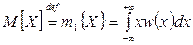. (4.4)

Приведём интерпретацию понятия среднего значения на примере дискретной случайной величины, принимающей конечное множество значений.

Пусть производится серия из 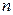независимых испытаний, в каждом из которых случайная величина 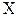принимает некоторое из допустимых значений 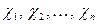, причём значение 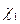принимается 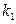раз, значение 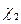принимается 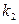раз, и так далее до некоторого значения 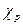, которое принимается 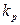раз. Очевидно, что 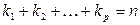. Тогда среднее арифметическое наблюдённых значений случайной величины 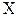, как известно, есть

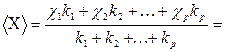
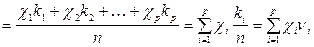. (4.5)

Здесь 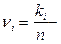относительная частота события 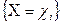. Если вероятность этого события обозначить через 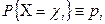, то в соответствии со статистическим определением вероятности при весьма большом числе испытаний 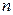получим 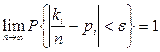. Поэтому при 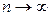из (4.5) имеем

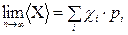. (4.6)

Сравнивая (4.6) с определением математического ожидания (4.4), получаем

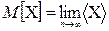. (4.7)

Предел в (4.6) и (4.7) понимается в вероятностном смысле.

Определение 4.4. Случайные величины 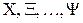называются независимыми, если закон распределения любой из них не зависит от того, какие возможные значения принимаются остальными.

Среднее арифметическое обладает рядом вполне очевидных свойств, которые легко получаются из определения (4.3):

;

;

;

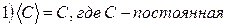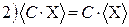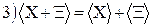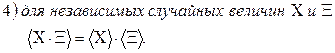
Имея в виду предельное соотношение (4.7), эти свойства постулируются и для математического ожидания произвольной случайной величины, а именно предполагается, что математическое ожидание удовлетворяет следующим аксиомам.

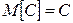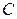М 1. , где – постоянная;

М 2. ;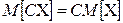

М 3. ;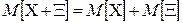

М 4. для независимых случайных величин .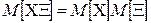

Пример 4.1. Производится серия независимых опытов, в каждом из которых может появиться или не появиться некоторое событие 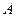с вероятностью 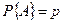. Пусть случайная величина 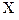– число появлений события 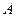в данной серии испытаний. Очевидно, что данная случайная величина распределена по биномиальному закону. Требуется найти математическое ожидание .

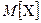Р е ш е н и е. Пусть 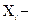характеристическая случайная величина события 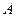, то есть случайная величина, равная числу появлений события 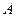в каждом опыте. Её закон распределения очевидным образом представляется в виде ряда распределения

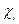
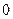
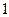
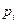
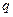
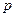
Здесь 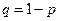. Поэтому, по определению математического ожидания дискретной случайной величины, имеем 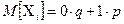. Так как наша случайная величина 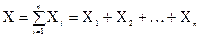, то для её математического ожидания получаем:

.

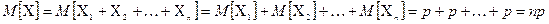Пример 4.2. Пусть дискретная случайная величина распределена по закону Пуассона. Требуется найти математическое ожидание этой случайной величины

Р е ш е н и е. По определению математического ожидания и в соответствии с таблицей 16.3.2, получаем

.

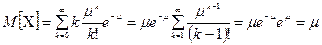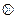
Центральные моменты распределения случайной величины. Рассмотрим теперь понятие центральных моментов случайных величин.

Определение 4.5. Пусть 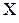– некоторая дискретная или непрерывная (всё равно) случайная величина. Центрированной случайной величиной, соответствующей случайной величине 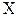, называется случайная величина 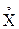, равная отклонению исходной случайной величины от её математического ожидания

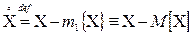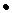. (4.8)

Определение 4.6. Центральным моментом распределения 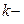го порядка случайной величины называется начальный момент 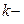го порядка соответствующей центрированной случайной величине .

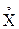Лемма 4.1. Математическое ожидание центрированной случайной величины равно нулю.

Д о к а з а т е л ь с т в о. Используя свойства математического ожидания, получаем:

.

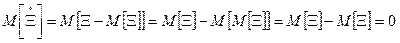Таким образом, первый центральный момент случайной величины 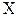равен нулю и, следовательно, не может служить характеристикой случайной величины. Для характеристики случайной величины используются её центральные моменты порядка .

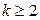В соответствии с определением 4.6 имеем:

для дискретной случайной величины

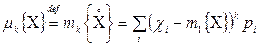; (4.9)

для непрерывной случайной величины

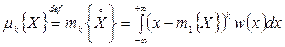. (4.10)

В (4.9) и (4.10) по лемме 4.1 нужно положить 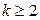. Из определения центральных моментов следует, что если среднее значение случайной величины 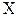равно нулю, то центральные моменты совпадают с начальными моментами. Таким образом, начальные моменты случайной величины 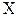– это моменты относительно нуля системы координат, а центральные моменты – это моменты относительно среднего значения этой случайной величины.

Дисперсия и среднеквадратическое отклонение. Из всех моментов 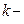го порядка случайной величины наиболее часто для её характеристики кроме среднего значения (математического ожидания) применяются дисперсия и среднеквадратическое отклонение.

Определение 4.7. Дисперсией случайной величины 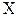(дискретной или непрерывной) называется её второй центральный момент.

Согласно определениям (4.7) и центральных моментов, для дисперсии имеем следующие выражения:

в случае дискретной случайной величины

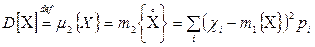; (4.11)

в случае непрерывной случайной величины

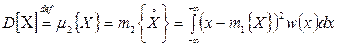, (4.12)

где для дисперсии случайной величины 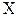, также как для математического ожидания, применено обычно используемое обозначение 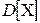. Можно показать, что дисперсия обладает свойствами, которые в общем случае, так же как для математического ожидания, мы примем за аксиомы:

. ;

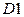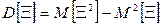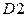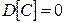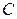. , где – постоянная;

. ;

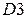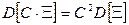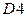. для независимых случайных величин 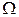и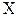

;

. .

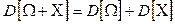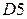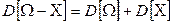Определение 4.8. Среднеквадратическим отклонением случайной величины 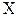называется положительное значение квадратного корня из её дисперсии (второго центрального момента).

Таким образом, согласно определению, имеем:

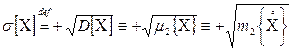. (4.13)

Дальше, согласно общепринятому соглашению, знак плюс перед квадратным корнем не пишется.

Пример 4.3. Пусть требуется вычислить дисперсию случайной величины 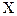из примера 13.2.1.

Р е ш е н и е. Используя определение дисперсии, получаем для характеристической случайной величины. :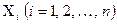

.

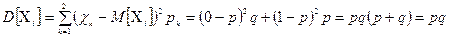Так как величины 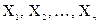независимы, для дисперсии 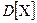получаем:

.

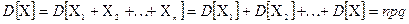Теперь получаем среднеквадратическое отклонение для случайной величины : .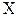

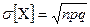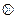
Пример 4.4. Воспользовавшись аксиомой 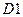, можно без особого труда показать, что дисперсия случайной величины, распределённой по закону Пуассона, равна: .

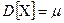Равномерный и нормальный законы распределения непрерывной случайной величины. Рассмотрим два типичных примера распределения непрерывных случайных величин, имеющих широкое распространение.

Определение 4.9. Если плотность вероятности 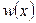некоторой непрерывной случайной величины 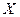имеет вид

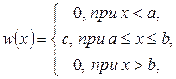(4.14)

то говорят, что случайная величина 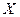распределена на промежутке 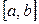равномерно.

Рассчитаем численное значение параметра 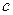в (4.14). Для этого вычислим интеграл, который равен

,

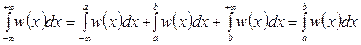так как первый и третий интегралы в силу (4.14) обращаются в нуль. В силу свойств плотности вероятности 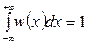. Из последних двух равенств получаем 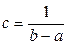. Теперь можно вычислить математическое ожидание непрерывной случайной величины, распределённой равномерно на промежутке 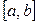. Имеем:

.

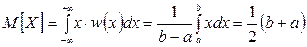Аналогично, легко получить дисперсию непрерывной случайной величины, распределённой равномерно на промежутке :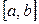

.

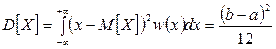Рассмотрим функцию

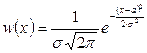, (4.15)

Проверим, что функция (4.15) удовлетворяет свойствам плотности вероятности. Из (4.15) очевидно, что 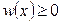при всех значениях 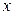. Проверим, что выполнение свойства 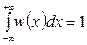. Для этого вычислим интеграл 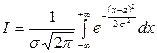. Производя замену переменной интегрирования 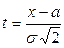, получаем:

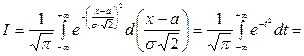
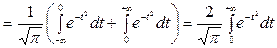. (4.16)

Последний интеграл называется интегралом Эйлера - Пуассона. Его вычисление даёт

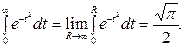
Подстановка в (4.16) даёт:

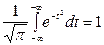, (4.17)

а значит, функция (4.14) действительно может служить плотностью вероятности некоторой случайной величины.

Определение 4.10. Если плотность вероятности непрерывной случайной величины 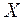имеет вид

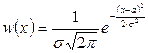, (4.18)

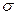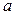где и – некоторые постоянные, причём 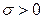, то говорят, что случайная величина 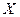распределена по нормальному, или гауссовскому закону. Случайная величина 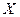в этом случае называется гауссовской.

Вычислим математическое ожидание случайной величины 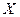, распределённой по нормальному закону (4.18). Имеем:

.

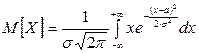Снова заменим переменную интегрирования по формуле 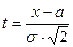, получим

,

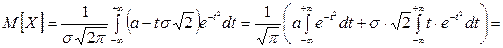
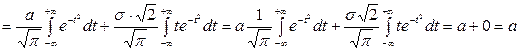где мы учли полученное выше значение интеграла (4.17) и справедливое в силу нечётности подынтегральной функции равенство . Таким образом, получаем:

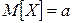. (4.19)

Аналогично, нетрудно показать, что

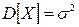
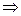
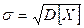. (4.20)

График плотности вероятности нормального распределения (4.18) имеет вид, представленный на рисунке 4.1.

Если математическое ожидание 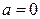и среднеквадратическое отклонение 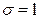, то нормальное распределение (4.18) называется нормированным. В этом случае плотность вероятности имеет вид

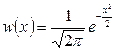. (4.21)

Вычислим вероятность попадания гауссовской случайной величины в промежуток 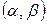. Для этого воспользуемся свойством (17.2.17) плотности вероятности, согласно которому вероятность попадания случайной величины 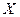в промежуток 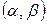выражается формулой

.

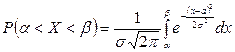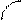
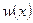
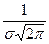
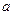
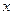
Рис. 4.1.

Произведём замену переменной интегрирования 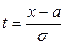, тогда получаем 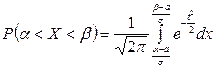. Вводя функцию 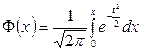, которая является первообразной для функции 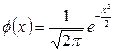и, используя формулу Ньютона-Лейбница, получаем:

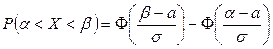. (4.22)

Дата добавления: 2014-01-20