Общие законы распределения случайных величин

Обеспечение высокой надежности технических систем на стадиях разработки, изготовления и эксплуатации зависит от многих факторов и условий, которые являются случайными величинами. Инженеры, занимающиеся разработкой, производством, испытаниями и эксплуатацией ВСТ, должны хорошо знать методологию определения, обработки и анализа случайных величин, влияющих на надежность различных изделий.

Примерами наиболее распространенных случайных величин, с которыми приходится иметь дело инженерам в своей практической деятельности, являются следующие:

- количество различных отказов, повреждений и время их возникновения, определяемое в единицах наработки или календарным временем при использовании, транспортировании и хранении изделий;

- показатели долговечности и сохраняемости отдельных изделий и их элементов: технический ресурс T_pi, срок службы T_слi, срок сохраняемости T_сi, полученные экспериментально или расчетом;

- показатели системы технического обслуживания и ремонта: продолжительность t_i, трудоемкость S_i, стоимость С_i, полученные по результатам натурных испытаний или наблюдений за конкретными образцами техники;

- время восстановления t_вi конкретных образцов и их отдельных составляющих: поиска неисправностей, разборочных, сборочных, восстановительных и регулировочных операций;

- характеристики различных свойств материалов: конструкционных, эксплуатационных, консервационных, используемых в различных условиях эксплуатации;

- параметры механических и электрических систем и их элементов, определяемые при изготовлении, техническом обслуживании и капитальном ремонте ВСТ.

Первичная информация об указанных случайных величинах может быть получена одним из следующих способов:

- наблюдением в течение определенного времени за изделием и его составными частями, находящимися в различных условиях и режимах эксплуатации, а также за состоянием различных материалов и климатических факторов в различных районах страны;

- организацией и проведением специальных натурных или ускоренных испытаний с изделиями, материалами в обычных (нормальных) или особых (экстремальных) условиях, причем такие испытания могут проводиться в процессе эксплуатации, производства и в лабораторных условиях;

- выборкой необходимых данных из технологической, эксплуатационной, ремонтной и другой документации (например, из формуляров, паспортов, актов испытаний, технических и контрольных осмотров, журналов и ведомостей диагностирования изделий и других документов).

Все случайные величины характеризуются законами их распределения.

Законом распределения случайной величины называется всякое соотношение, устанавливающее связь между возможными значениями случайной величины и соответствующими им вероятностями.

Случайные величины могут быть дискретными (прерывными) и непрерывными. Возможные значения дискретных величин могут быть заранее перечислены. Возможные значения непрерывных величин не могут быть заранее перечислены и непрерывно заполняют некоторый промежуток.

Примером дискретной случайной величины может служить число отказов однотипных элементов за промежуток времени t. Если в узле имеется 3 детали, то число отказов может быть 0,1,2,3.

Простейшей формой задания закона распределения дискретной случайной величины является таблица, в которой перечислены возможные значения случайной величины q_i и соответствующие им вероятности Р_i (табл.3.1).

Таблица 3.1

Ряд распределения

qi
Рi	Р0	Р1	Р2	Р3

Такая таблица называется рядом распределения дискретной случайной величины.

Примером непрерывной случайной величины может служить время отказа элемента. Составить таблицу, в которой были бы перечислены все значения времени отказа, невозможно.

Поэтому для характеристики случайного времени отказа выбирается вероятность того, что случайное время отказа q будет меньше времени t. Эта вероятность будет являться функцией времени t. Если время будет стремиться к нулю, то и вероятность отказа за время t будет стремиться к нулю. При увеличении времени работы элемента вероятность отказа естественно будет увеличиваться.

Функцией распределения случайной величины q называется вероятность того, что случайная величина q примет значение меньше t

F(t)=p(q < t), (3.1)

где F(t) - функция распределения случайной величины q;

p(q< t) - вероятность того, что случайная величина q меньше заданного значения t. Поскольку случайной величиной является время отказа, то время t может меняться от 0 до ∞.

Функция распределения является неубывающей функцией и обладает следующими свойствами:

F(t=0)=0; F(t=∞)=1. (3.2)

Функция распределения называется еще интегральным законом распределения случайной величины q.

Общий вид функции распределения и ее плотности показан на рис.3.1.

Зная интегральный закон распределения (рис. 3.1,а), можно найти вероятность попадания случайной величины на заданный участок.

Выделим небольшой участок ∆t. Вероятность того, что случайная величина q попадает на участок ∆t равна F(t+∆t)-F(t).

Вероятность того, что случайная величина q попадает на единицу длины участка ∆t равна 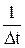.[F(t+Dt)-F(t)].

Если примем, что ∆t→0, то получим производную от функции распределения f(t)

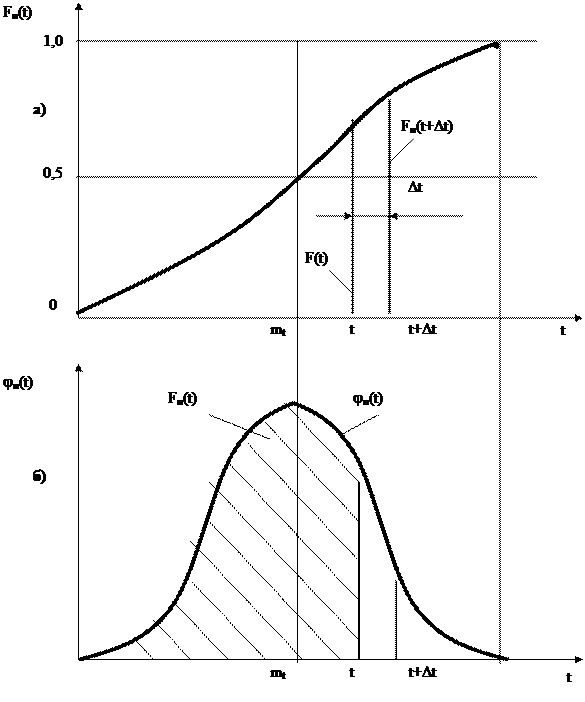Рис.3.1. Графическая интерпретация функции F_н(t) и плотности j_н(t) распределения для нормального закона:

а) функция распределения F_н(t); б) плотность распределения j_н(t)

f(t)=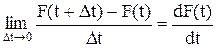=F^’(t).

Функция f(t) называется дифференциальным законом распределения или плотностью вероятности случайной величины q. Дифференциальный и интегральный законы распределения связаны зависимостями:

f(t)=F^’(t), F(t)= 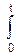f(t)dt. (3.3)

Дата добавления: 2014-01-20