
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Используемые при оценке надежности
|
|
|
|
Основные виды теоретических законов распределения,
В теории надежности наиболее часто применяется экспоненциальный закон. При этом функция распределения имеет вид (рис.3.2,а)
F(t)=1-exp(-lt), (3.11)
где λ - параметр распределения (величина постоянная).
В дифференциальной форме экспоненциальный закон имеет следующий вид:
f(t)=lexp(-lt).(3.12)
Найдем математическое ожидание и дисперсию случайной величины, распределенной по экспоненциальному закону:
mt=  tf(t)dt=l
tf(t)dt=l te-ltdt=
te-ltdt=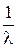 , (3.13)
, (3.13)
Dt= (t-mt)2f(t)dt=
(t-mt)2f(t)dt= (t-
(t-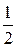 )2le-ltdt=
)2le-ltdt=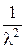 , (3.14)
, (3.14)
 . (3.15)
. (3.15)
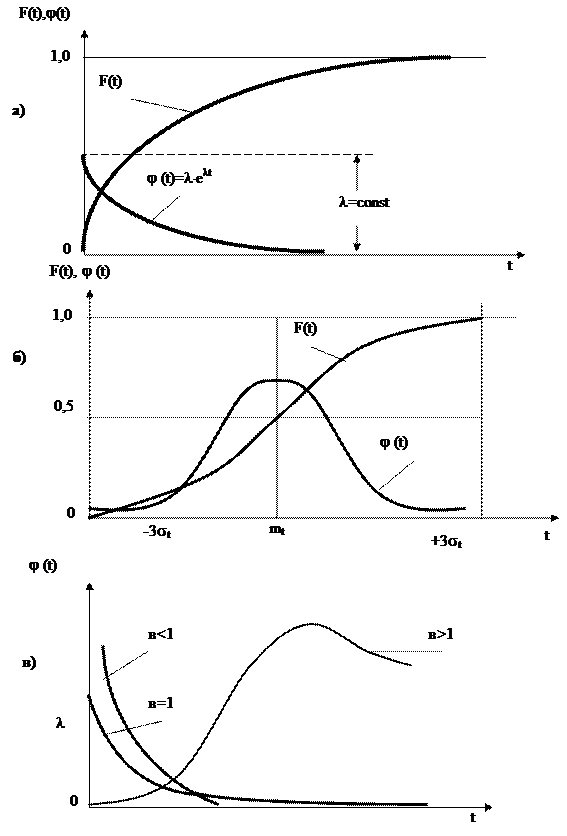
Рис.3.2. Графическая изображение частных законов распределения:
а) экспоненциальный закон; б) нормальный закон; в) закон распределения Вейбулла.
По экспоненциальному закону распределяется время внезапных отказов пультовой аппаратуры, механических и гидравлических систем в рабочем режиме, эксплуатации, а также время внезапных и постепенных отказов сложных изделий при хранении изделий на базах и складах и при транспортировании их по железной дороге и другими видами транспорта.
Время износовых (постепенных) отказов элементов гидравлических и механических систем, а также некоторых элементов электрических систем иногда подчиняется нормальному закону.
В частности, нормальное распределение времени отказов следует ожидать в тех случаях, когда обеспечивается достаточная однородность качества элементов, а скорость износа зависит от большого числа факторов, ни один из которых не является преобладающим.
Нормальный закон (рис. 3.2,б) может быть выражен одной из зависимостей:
F(t)=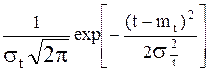 dt, (3.16)
dt, (3.16)
f(t)=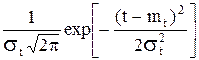 , (3.17)
, (3.17)
где mt - математическое ожидание случайной величины t,
st - среднее квадратическое отклонение.
Интеграл типа  не выражается через элементарные функции и поэтому для его вычисления пользуются таблицами Лапласа (интеграла вероятностей)
не выражается через элементарные функции и поэтому для его вычисления пользуются таблицами Лапласа (интеграла вероятностей)
Ф(t)= dz. (3.18)
dz. (3.18)
Нормальный закон распределения через интеграл вероятностей выражается
F(t)=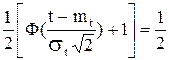 [Ф(z)+1]. (3.19)
[Ф(z)+1]. (3.19)
График нормального закона показан на рис 3.2,б. Экспоненциальный и нормальный законы являются частными случаями более общего закона гамма-распределения. При этом распределении плотность вероятности выражается формулой
f(t)=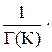 lktk-1e-lt, (3.20)
lktk-1e-lt, (3.20)
где Г(К) – гамма-функция, определяемая формулами:
Г(К)= , при К<1, Г(К)=(К-1)Г(К-1), при К>2, (3.21)
, при К<1, Г(К)=(К-1)Г(К-1), при К>2, (3.21)
где значения Г(К) определяются по таблицам.
Если учесть, что для целых К справедливо соотношение
Г(К)=(К-1)!,
то можно записать:
f(t)=l e-lt, (3.22)
e-lt, (3.22)
где λ и К - параметры гамма-распределения.
При К=1 гамма-распределение превращается в экспоненциальное распределение, а при К→ ∞ - в нормальное распределение.
Найдем математическое ожидание и дисперсию случайной величины, подчиненной гамма-распределению.
mt= tf(t)dt=
tf(t)dt=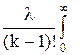 t(lt)k-1e-ltdt=
t(lt)k-1e-ltdt=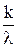 , (3.23)
, (3.23)
Dt= (t-mt)2f(t)dt=
(t-mt)2f(t)dt= (t-
(t-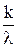 )2
)2  e-ltdt=
e-ltdt= . (3.24)
. (3.24)
Гамма-распределению подчиняется время возникновения отказов сложных электрических систем на начальной стадии их эксплуатации, а также сложных резервированных систем. Время отказов при приработке элементов подчиняется иногда гамма-распределению при К<1.
Наиболее общим законом является также и распределение Вейбулла. Этот закон определяется следующими формулами:
F(t)=1-exp(-ltb), (3.25)
f(t)= λ btb-1exp(-ltb), (3.26)
где λ - параметр масштаба (размерная величина),
b - параметр формы (безмерная величина).
Числовые характеристики для закона Вейбулла определяются по формулам:
mt= Г(1+b-1), (3.27)
Г(1+b-1), (3.27)
Dt=l-2{Г(1+2b-2)-[Г(1+b-1)]2}, (3.28)
Г(·) - гамма-функция определяется по таблицам.
Легко заметить, что при b=1 распределение Вейбулла превращается в экспоненциальное распределение, а при b=3,25 оно приближается к нормальному. Характер изменения функции f(t) при различных значениях b показан на рис. 3.2,в.
Распределение Вейбулла хорошо описывает распределение времени безотказной работы многих элементов радиоэлектронной аппаратуры (ламп, транзисторов, некоторых пультов) в случае, когда отказ этих элементов рассматривается как выход какого-либо их параметра за установленные пределы.
Кроме этого, иногда применяется распределение Релея
f(t)= , (3.29)
, (3.29)
где st- параметр закона (постоянная величина).
Логарифмическое нормальное распределение:
f(t)= , (3.30)
, (3.30)
где mу , σу –параметры закона, (mу = lg mt; σу = lg σt).
Заключение
Проблема оценки надежности технических систем является комплексной. Её различные аспекты связаны с изучением физических процессов, приводящих к отказам, с экспериментальными исследованиями, с огромным числом эксплуатационных факторов, включающих и подготовку технического персонала. Она базируется на математических методах и моделях, характеризующих распределение вероятностей интервалов безотказной работы и интервалов восстановления систем, и для их усвоения от обучающихся требуется общая математическая подготовка, не выходящая за пределы программы технического вуза.
|
|
|
|
Дата добавления: 2014-01-20; Просмотров: 268; Нарушение авторских прав?; Мы поможем в написании вашей работы!