Преобразования координат Галилея. Механический принцип относительности

Лекция 6 Элементы релятивистской механики

Преобразования Галилея. Механический принцип относительности. Постулаты специальной теории относительности. Преобразования Лоренца. Относительность длин и промежутков времени. Релятивистский импульс. Релятивистское выражение для кинетической энергии. Соотношение между полной энергией и импульсом частицы. Взаимосвязь массы и энергии.

Механика Ньютона, или, как говорят, классическая механика, основана на принципе относительности Галилея, согласно которому все законы механики одинаковы во всех инерциальных системах отсчета.

Математически принцип относительности в классической механике выражается с помощью преобразования Галилея — закона сложения скоростей при переходах от одной инерциальной системы отсчета к другой. Согласно этому закону скорость тела в неподвижной системе отсчета представляет собой сумму скорости тела по отношению к движущейся системе отсчета и скорости самой системы отсчета по отношению к неподвижной.

Все законы физики имеют одинаковый вид во всех инерциальных системах отсчета. Другими словами: все инерциальные системы физически эквивалентны друг другу и понятия абсолютного движения и абсолютного покоя лишены смысла.

Этот фундаментальный закон выражает тот опытный факт, что два любых опыта, поставленных одинаковым образом в двух разных инерциальных системах, дают одни и те же результаты, т.е. являются объективным отражением природы.

Поскольку физические законы обычно формулируются как количественные соотношения между различными физическими величинами и записываются в виде математических уравнений, принцип относительности утверждает неизменность (инвариантность) уравнений относительно перехода из одной инерциальной системы координат в другую.

Очевидно, что в физике должны существовать величины как относительные, так и абсолютные.

Рассмотрим последнее утверждение на примере преобразования координат Галилея. Пусть имеются две прямоугольных системы координат (x,y,z,t) и (x`,y`,z`,t`), причем система (x`,y`,z`,t`) движется с постоянной скоростью V вдоль оси х системы (x,y,z,t), как на рис 1.

z

t z` · M t`

V

x x`

O O`

y y`

Рисунок 1. К выводу преобразований координат Галилея

Определим координаты точки М в движущейся и неподвижной системах координат.

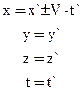
Этот набор уравнений учитывает возможность движения подвижной системы как в положительном, так и в отрицательном направлении оси х, а также тот факт, что в классической механике время во всех системах движется одинаково – длительность секунды везде одинакова.

Продифференцируем этот набор уравнений по t.

.

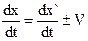По определению, 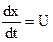– скорость движения точки М относительно системы координат (x,y,z,t), а 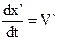– скорость движения т.М относительно системы координат (x`,y`,z`,t`).

Таким образом,

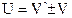, то есть скорость поступательного движения точки (тела) есть величина относительная.

Продифференцируем последнее соотношение еще раз:

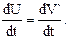
Поскольку по определению 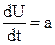– ускорение т.М в неподвижной системе координат, и 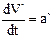– ускорение т.М в подвижной системе координат и а = а`, то, очевидно, следует считать, что ускорение является величиной абсолютной.

Поскольку в классической механике масса тела – также величина абсолютная, то абсолютной является и величина силы:

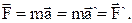
Понятно, что и уравнения движения, обязанного этим силам, будет одинаковым в любых инерциальных системах координат.

Не трудно показать, что абсолютной величиной в классической физике является также длина отрезка, пространственного промежутка. Пусть в неподвижной системе координат находится прямой абсолютно твердый стержень с координатами концов (x₁,y₁,z₁) и (x₂,y₂,z₂). Его длина L равна

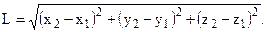
Используя преобразования координат Галилея, можно показать, что

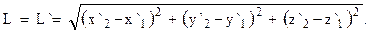
(x`<sub>1</sub>,y`₁,z`<sub>1</sub> и x`₂,y`<sub>2</sub>,z`₂, - координаты концов стержня в подвижной системе координат, все члены, содержащие произведение vt, сократятся).

Дата добавления: 2014-01-20