Релятивистское выражение для кинетической энергии

Релятивистский импульс

Выражение, обеспечивающее инвариантность закона сохранения импульса, может быть получено, если вместо времени t подставить собственное время τ.

Тогда .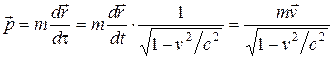

В релятивистской механике справедливым остается выражение

.

Это означает, что 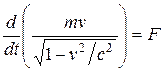. Откуда видно, что сила не является инвариантной величиной. Кроме того, сила F и ускорение a не коллениарны.

Легко получить выражение для кинетической энергии.

Пусть тело (частица) ускоряется при прямолинейном движении вдоль постоянной силой F, работа которой будет трансформироваться в прирост кинетической энергии

,

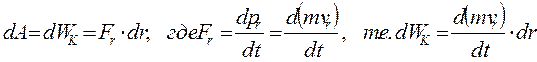причем мы не можем, как раньше, выносить m за знак дифференцирования как константу, потому что при v~c m¹const. Поскольку 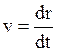, поменяем порядок дифференцирования по координате

Рассмотрим теперь подробнее релятивистское выражение для массы

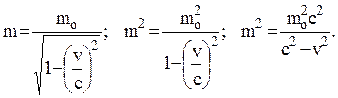
Упростим последнее выражение:

m²c² – m²v² = m_o²c²Þ m²c² = m_o²c² + m²v²

и продифференцируем с учетом условия m_o = const и c=const:

2c²m×dm = 2mv²dm + 2m²v×dv½: 2m.

Получаем

с²dm = v²dm + mv×dv.

Сравним правые части уравнений и приравняем левые части этих уравнений

dW_K = c²dm.

Проинтегрируем это равенство c учетом, что при v = 0 W_K = 0, m = m_o

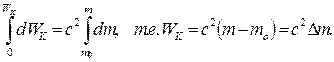
Итак,

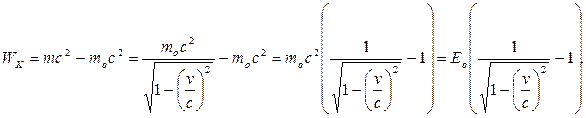
Понятно, что Е_о = m_oc² – энергия покоя тела, а mc² – полная энергия тела, а их разность W_K и есть кинетическая энергия, энергия, обусловленная движением тела.

Следствия:

1) Выражение Е_о =m_oc², впервые полученное Эйнштейном, характеризует полный запас энергии, содержащийся в любом теле.

2) Из релятивистского соотношения кинетической энергии привычное 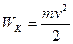может быть легко получено при v<<c

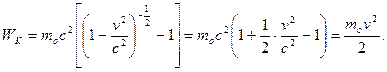
При релятивистском движении иначе выглядит и уравнение связи импульса частицы с её кинетической энергией

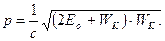
Энергия и импульс в релятивистской механике не сохраняются. Инвариантом является выражение:

6.7 Взаимосвязь массы и энергии покоя

Масса тела и его энергия покоя связаны соотношением Е₀ = т₀с². Можно сделать важный вывод, что всякое изменение массы Δт сопровождается изменением энергии покоя ΔЕ₀, при чем эти изменения пропорциональны друг другу.

ΔЕ₀=с² Δт.

Это утверждение носит название закона взаимосвязи массы и энергии покоя (иногда говорят просто массы и энергии).

Взаимосвязь т и Е₀ приводит к тому, что суммарная масса взаимодействующих частиц не сохраняется.

Рассмотрим пример неупругого центрального удара двух одинаковых
частиц, движущихся с равными по модулю и противоположными по направлению скоростями. В результате соударения образуется новая
неподвижная частица. В ньютоновской механике мы бы имели

M=m+m=2m; V=V_l-V₂=0 (|V₁|= |V₂|)

В релятивистской механике дело обстоит несколько иначе:

1) до соударения полная энергия каждой частицы равна

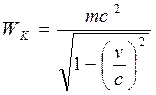
2) полная энергия образовавшейся неподвижной частицы

Е=Мс²

3) Применим закон сохранения энергии к данному случаю

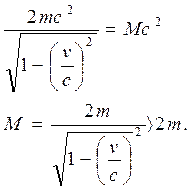
Таким образом, масса образовавшейся частицы больше масс исходных частиц. Это обусловлено тем, что кинетическая энергия частиц превратилась в эквивалентное количество энергии покоя, а это привело, в свою очередь, к возрастанию массы на

Δт = ΔЕ₀/с².

Если обобщить вышесказанное на произвольный случай движения частиц с околосветовыми скоростями, то можно записать

Е₀ = т₀с²,

где т₀ - масса покоящейся частицы или масса покоя частицы, V - скорость движущейся частицы.

Тогда масса движущейся частицы m будет равна

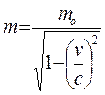
При распаде неподвижной частицы на несколько разлетающихся в разные стороны частиц наблюдается обратное явление - сумма масс образовавшихся частиц оказывается меньше исходной частицы на величину, равную суммарной кинетической энергии этих частиц, деленной на с².

Если обобщить наши выводы на тело, состоящее из N частиц с массами т₁т₂...т_N, то тело не будет распадаться на образующие его частицы при условии, что последние связаны друг с другом. Эту связь можно охарактеризовать энергией связи Е_св. Энергия связи - это энергия, которую

нужно затратить, чтобы разорвать связь между частицами и разнести их на такие расстояния, при которых взаимодействием частиц можно пренебречь.

Энергия связи системы частиц будет равна

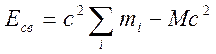
где М - масса системы (масса тела).

Дата добавления: 2014-01-20