Сила давления жидкости на плоские стенки

Сначала рассмотрим силы давления жидкости на горизонтальные стенки.

Сила давления жидкости на горизонтальное дно сосуда определяется по формуле (рис. 1.9):

, (1.19)

а давление на дно, согласно основному уравнению гидростатики, как:

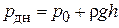. (1.20)

Рис. 1.9. Сила давления жидкости на горизонтальные стенки

Следовательно, сила давления жидкости на горизонтальное дно зависит от давления на свободной поверхности , плотности жидкости r, глубины погружения поверхности h, но не зависит от формы сосуда (гидростатический парадокс).

Рассмотрим более общий случай. Пусть площадь 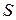расположена под углом 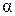к горизонту и перпендикулярна к плоскости рисунка (рис. 1.10).

Через проекцию контура площади S (линия АВ) проведем ось оу
и спроектируем эту площадь на плоскость хоу.

Определим силу давления жидкости на элементарную площадку предполагая, что в пределах давление не меняется:

Здесь – давление на свободной поверхности, h – глубина погружения площадки dS. Заметим, что . Для определения полной силы 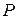проинтегрируем полученное выражение по всей
площади S.

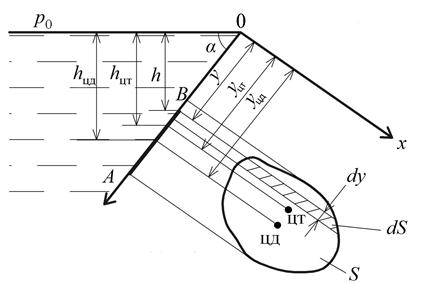
Рис. 1.10. Схема для определения силы давления жидкости

на плоскую стенку

Последний интеграл в правой части уравнения представляет собой статический момент площади 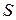относительно оси ох и равен:

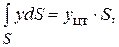
где – координата центра тяжести площади 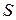. Заменяя получим:

(1.21)

Здесь 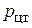– давление в центре тяжести площади S. Полная сила давления на плоскую стенку равна произведению площади стенки на гидростатическое давление в центре тяжести этой площади.

Формулу (1.21) представим в другом виде:

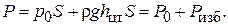(1.22)

Здесь – внешняя сила, 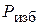– избыточная сила, вызванная весом жидкости.

Внешнее давление передается всем точкам площади S одинаково, поэтому внешняя сила будет приложена в центре тяжести площади S. Сила избыточного давления 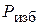из-за неравномерности распределения избыточного давления по глубине приложена ниже в центре давления.

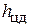Координата центра гидростатического давления определяется по формуле:

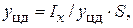(1.23)

где 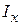– момент инерции фигуры 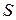относительно оси ох.

Зависимость (1.23) может быть представлена в виде:

(1.24)

где 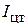– момент инерции фигуры S относительно оси, проходящей через её центр тяжести. Величина представляет собой эксцентриситет.

Зная величины и 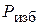и точки их приложения, можно найти величину и точку приложения общей силы P.

Дата добавления: 2014-01-20