Закон Архимеда. Сила давления жидкости на криволинейные стенки

Сила давления жидкости на криволинейные стенки.

В отличие от плоской стенки, элементарные силы, действующие
на элементарные площадки криволинейной стенки в различных точках, различаются не только по величине, но и по направлению. Поэтому силу гидростатического давления, действующего на криволинейную стенку, непосредственно определить невозможно, его находят через составляющие (проекции) этой силы.

Для простоты рассмотрим цилиндрическую поверхность аb
с образующей, перпендикулярной к плоскости чертежа (рис. 1.11). Жидкость действует на стенку аb с силой 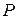, а стенка аb с такой же силой, но в обратную сторону. Разложим эту силу 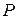на вертикальную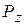
и горизонтальную 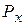составляющие.

Далее рассмотрим условие равновесия объема жидкости, заключенного в вертикальном направлении в отсеке abcd:

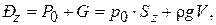(1.25)

где 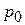– давление на свободной поверхности, 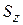– проекция площади S на горизонтальную (свободную) поверхность, V – объем жидкого тела. Объем жидкого тела (тело давления) ограничено снизу криволинейной поверхностью аb, сверху – проекцией этой поверхности на свободную поверхность cd, а с боков – цилиндрической поверхностью, полученной
в результате проектирования площади S на свободную поверхность. Необходимо отметить, что V не всегда представляет объем жидкости.

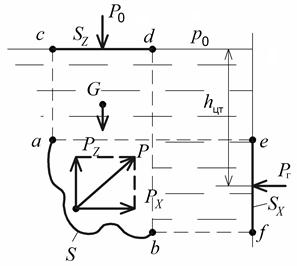
Рис. 1.11. Схема для определения силы давления жидкости
на криволинейную (цилиндрическую) стенку

Определим горизонтальную составляющую 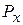. На некотором расстоянии по горизонтали от площади S жидкость условно разрезаем
в вертикальной плоскости и правую часть отбрасываем. На вертикальную стенку спроектируем площадь S и получим .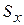

Реакцию отброшенной части жидкости обозначим через 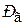. Далее рассмотрим равновесие объема жидкости, заключенной между плоскостями аb и ef. Заметим, что сила 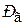является силой давления
на плоскую стенку :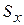

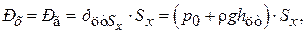(1.26)

где 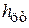– глубина погружения центра тяжести площади 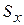, 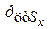– давление в центре тяжести площади .

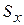Полную силу находим по формуле:

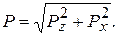(1.27)

Тогда положение силы 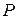находится графическим путем как точка пересечения направления силы 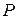с криволинейной поверхностью.

В общем случае полная сила определяется по формуле:

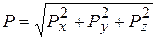. (1.28)

В этом случае 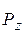определяется по формуле (1.25), 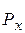– по формуле (1.26). Сила 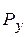, как и сила 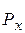, расположена в горизонтальной плоскости и определяется по формуле, аналогичной (1.26).

Закон Архимеда. Рассмотрим полностью погруженное в жидкость твердое тело (рис. 1.12).

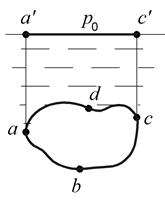
Рис. 1.12. Тело, покоящееся в жидкости

Горизонтальные составляющие силы 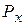и 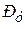полностью уравновешиваются. Рассмотрим вертикальную составляющую .

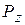Вертикальная сила, действующая на нижнюю поверхность аbс больше вертикальной силы давления на верхнюю поверхность adc. Разность вертикальных сил, согласно формуле (1.25), получим в виде:

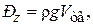(1.29)

где 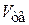– объем твердого тела, r – плотность жидкости.

Итак, на тело, погруженное в жидкость, действует гидростатическая подъёмная сила, направленная вверх и численно равная силе тяжести вытесненной им жидкости. Точка приложения гидростатической подъемной силы – центр тяжести вытесненного объема жидкости.

Дата добавления: 2014-01-20