Введение в теорию игр. Неформальное описание игры

Проект защиты.

Содержит требования и задача защиты ИТ-продукта, а также описывает уровень функциональных возможностей, реализованных в нем средст защиты, их обоснование и подтверждение степени их адекватности. Необходим для разработчика и является эталоном в ходе квалификационного анализа.

1) Введение:

• идентификатор (уникальное название);

• обзор содержания.

2) Раздел требований безопасности:

• раздел функциональных требований (типовые и специфицеские требования);

• раздел требований адекватности (включает уровни не представленные в Единых критериях и представленные в Единых критериях).

3) Общие спецификации ИТ-продукта:

• описывают механизмы осуществления задач зашиты с помощью определения высокоуровневых спецификаций средств защиты.

4) Заявка на соответствие профилю защиты

5) Обоснование:

• содержит полное и связное множество требований и реализаций. Его ИТ-продукт будет эффективно противостоять угрозам безопасности действующим в среде его эксплуатации, и содержит подтверждение соответствия профилю защиты.

Оба документа определяют технологию разработки защищенных систем.

В России аутентичный перевод «Общих критериев» версии 2.0 принят в качестве ГОСТ в 2002 г. и введен в действие с 1 января 2004 г. Точное название докумен­та — ГОСТ Р ИСО/МЭК 15408-2002 «Информационная технология. Методы и средства обеспечения безопас­ности. Критерии оценки безопасности информацион­ных технологий».

Документ состоит из трех частей [33-35]:

1. Введение и общая модель.

2. Функциональные требования безопасности.

3. Требования доверия к безопасности.

В перспективе «Общие критерии» должны заменить РД Гостехкомиссии России во всех системах сертифика­ции средств защиты информации. В настоящий момент оба поколения стандартов используются одновременно, причем «Общие критерии» применяются исключительно при проведении сертификации продуктов, не предназна­ченных для обработки информации, составляющей госу­дарственную тайну

Т еория игр была основана Джоном фон Нейманом и Оскаром Моргенштерном в их первой работе «The Theory of Games and Economic Behavior», изданной в 1944 году. В 1928 году в математических анналах фон Нейманом была опубликована статья «О теории общественных игр», в которой впервые было применено понятие «теория игр». Использование этого понятия объясняется схожестью логики принятия решений в таких играх, как шахматы, скат или покер, и в некоторых ситуациях общественной жизни, прежде всего в экономике и военном деле. Характерным для таких ситуаций является то, что результат для принимающего решение зависит не только от его решения, но и от того, какое решение примут другие. Поэтому оптимальный исход не может быть получен в результате принятия решения одним лицом.

Математическая дисциплина, исследующая ситуации, в которых принятие решений зависит от нескольких участников, называется «теорией игр», потому что вполне аналогичные с математической точки зрения положения возникают в общеизвестных «салонных» играх (например, в таких, как покер, бридж, шахматы, игра в крестики и нолики и другие). Область приложения теории игр выходит, конечно, далеко за рамки таких игр и включает, например, математику, экономику, политику, военную стратегию. Однако в терминологии теории игр много заимствований из терминологии общеизвестных игр.

Ситуации, рассматривающиеся в теории игр, содержат следующие элементы:

• n играющих, n>1;
• правила игры;
• выплаты игрокам: они могут быть положительные и отрицательные;
• информация игроков.

Структура последнего элемента раскрывается следующей схемой:

Лица, принимающие решения, называются игроками, а целевая функция – платежной функцией. Под игроками могут подразумеваться отдельные лица или группы лиц (как, например, партнеры по игре в бридж), фирмы, страны и т.д. Выигрыш каждого игрока определяется платежной функцией.

ОПР. Таким образом, игра представляет собой совокупность известных всем игрокам правил, которые определяют, что может делать игрок и каковы последствия и выигрыши в результате каждого отдельного их действия.

Основные понятия в теории игр:

• Ход – это момент игры, когда происходит принятие решения одним из игроков.
• Партия – проведение одной игры, некоторая определенная совокупность ходов и выборов. Существенной чертой любой игры является то, что выигрыш каждого игрока зависит обычно не только от сделанного им самим выбора, но и от выбора других игроков. Каждый игрок должен учитывать эту зависимость от остальных игроков при выборе стратегии.
• Cтратегия – полное описание поведение игрока при каждом его решении в рамках правил игры и имеющейся у него информации. Так как понятие стратегии является в теории игр центральным, то эту дисциплину нередко называют «стратегическими играми».

Всякая игра предполагает следующее:

1. Наличие некоторого числа n участвующих в ней лиц (игроков). Могут быть игры с одним игроком (пасьянс), двумя игроками (шахматы, муж с женой, две конкурирующие фирмы), тремя игроками (преферанс, три фирмы на рынке) и т.д. По числу игроков и идёт классификация игр -- игры двух лиц, трёх лиц и т.д.;

2. Конечный выигрыш (или проигрыш) каждого игрока. Когда игра кончается, каждый игрок получает доход p_i (если p_i <0 – значит, игрок проиграл), зависящий от его поведения и поведения других игроков.

Различные виды игр можно классифицировать, основываясь на том или ином принципе: по числу игроков или по числу стратегий, по свойствам платежной функции или по характеру предварительных переговоров между игроками до игры.

1. В зависимости от числа игроков различают игры с двумя, тремя и более участниками.

При наличии двух игроков могут возникать и конфликтные ситуации, и необходимость в координированных действиях (кооперация). Когда число игроков не меньше трех, могут создаваться коалиции – группы из двух или более игроков, имеющих общую цель и координирующих свои стратегии.

2. Согласно другому принципу классификации – по количеству стратегий – различают конечные и бесконечные игры.

Игры, в которых один или несколько игроков располагает бесконечным числом стратегий, называют бесконечными играми.

3. Третий способ классификации игр – по свойствам платежной функции. Одним из важных типов платежных функций является платежная функция в игре с нулевой суммой, когда общая сумма выигрышей игроков равна нулю (игры с нулевой суммой называют также антагонистическими). В игре двух участников с нулевой суммой выигрыш одного из партнеров равен проигрышу другого, т.е. налицо прямой конфликт между игроками. Прямой противоположностью играм такого типа являются игры двух участников с постоянной разностью, в которых игроки и выигрывают, и проигрывают одновременно, так как им выгодно действовать сообща. В общей игре с ненулевой суммой имеют место, как правило, и конфликты, и согласованные действия игроков.

4. В зависимости от характера предварительной договоренности между игроками различают кооперативные и некооперативные игры. Игра называется кооперативной, если до начала игры игроки образуют коалиции и принимают взаимообязывающие соглашения о своих стратегиях. Игра, в которой игроки не могут координировать свои стратегии подобным образом, называется некооперативной.

Существует ряд способов описания и анализа конкретных игр. Один из приемов описания игры состоит в том, что указывает, какие ходы могут делать игроки, какой информацией во время игры они располагают, какие варианты можно выбирать и какими могут быть предельные размеры платежей в конце игры. Игра, описанная таким образом, называется игрой в развернутой (экстенсивной) форме, а само описание составляется в виде дерева игры. Например:

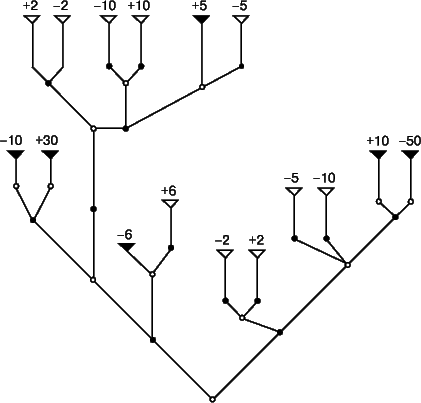
Игра в развернутой форме является игрой с полной информацией, если в ней нельзя делать одновременно несколько ходов, и если участникам известны выборы, сделанные в предшествующих ходах, включая и случайные ходы. Примерами игр с полной информацией является шахматы и игра в крестики и нолики. Покер, напротив, представляет собой игру с неполной информацией, так как игрокам не известны некоторые выборы, сделанные при случайных ходах, - прежде всего им не известно, какие карты находятся на руках у противника.

Другой способ описания игры состоит в том, что рассматриваются все возможные стратегии каждого игрока и определяются платежи, соответствующие любой возможной комбинации стратегий всех игроков.

Описанная таким образом игра называется игрой в нормальной форме. Зная развернутую форму игры, можно получить и ее нормальную форму.

Наиболее изученным классом игр являются так называемые игры с нулевой суммой, когда в любой партии имеет место условие:

,

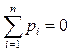то есть если кто-то выигрывает, то кто-то обязательно проигрывает. Это особенно проявляется в играх двух лиц с нулевой суммой, когда p₁ + p₂ =0, то есть p₁ = - p₂. В этом случае интересы игроков строго противоположны, так как выигрыш одного игрока является одновременно проигрышем другого.

Основное содержание современной теории игр –- это так называемая матричная форма игры. В этом случае считается, что каждый игрок делает всего лишь один ход, причем все ходы делаются одновременно. После этого каждому игроку выплачивается выигрыш (или берётся проигрыш) в зависимости от того, какие ходы были сделаны им и другими игроками.

Вообще говоря, игра в позиционной форме (представленная в виде последовательности ходов) может быть сведена к игре в матричной форме, однако для реальных игр это сведение настолько сложно, что практически невыполнимо даже для современных ЭВМ. Однако вполне возможно, что в будущем такое сведение будет иметь и практический смысл.

Дата добавления: 2014-01-20