Игры с седловой точкой

Рассмотрим с этих позиций игру со следующей платёжной матрицей:

.

Рассмотрим рассуждения, которыми руководствуется первый игрок. Если он сделает ход i=1, то наихудшей для него будет ситуация, когда второй игрок сделает ход j=3, так как в этом случае он получит 0. Если первый игрок сделает ход i=2, то в наихудшем случае (при ходе второго игрока j=1) он также получит 0. Аналогично, при i=3 он в наихудшем случае получит 4 (при j=2), при i=4 - 2 (при j=3) и, наконец, при i=5 он в наихудшем случае получит 0 (при j=3).

Стремясь сделать свой гарантированный выигрыш как можно больше, первый игрок должен выбрать ход i=3, так как в этом случае он гарантирует себе выигрыш, равный 4 (правда, и его максимальный выигрыш невелик - всего 5).

А теперь попробуем посмотреть на эту же матрицу с точки зрения второго игрока. Для него это –- матрица его проигрыша.

Если он выберет ход j=1, то его максимальный проигрыш будет равен 18 (если первый игрок сделает ход i=1). Аналогично, при j=2 его максимальный проигрыш будет равен 4, при j=3- – 8, и, наконец, при j=4 его максимальный проигрыш будет равен 25. Стремясь сделать свой максимальный проигрыш как можно меньше, второй игрок должен выбрать ход j=2, так как в этом случае его максимальный проигрыш, равный 4, самый маленький.

Итак, мы пришли к выводу, что первый игрок должен ходить i=3, а второй j=2. Допустим теперь, что второй игрок, как говорят, «открывает карты» и заявляет первому игроку: «Я буду делать ход j=2». Есть ли первому игроку необходимость менять свой ход? Нет, так как в этом случае его наилучший ход всё равно i=3.

Аналогично, если первый игрок заявит второму, что он будет ходить i=3, то второму игроку также нет смысла менять свой ход, так как наилучшим ответом будет всё равно j=2. Пара i=3, j=2 является, как говорят, уравновешенной парой, так как «открытие карт» игроками не даёт поводов противнику менять свою стратегию. Как говорят, пара i=3, j=2 есть решение игры, а величинавыигрыша при этом первого игрока (и одновременно величина проигрыша второго) - 4 – это цена игры.

Оформим всё это математически. Итак, пусть первый игрок выбирает ход i. В наихудшей для него ситуации он выиграет:

.

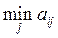Стремясь сделать свой минимальный выигрыш максимальным, он выбирает свой ход из условия:

.

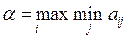Такая стратегия называется максиминной, а величина α называется нижней ценой игры, или максимином.

Аналогично, второй игрок, выбирая ход j, в наихудшей для себя ситуации проигрывает:

.

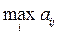Стремясь сделать свой максимальный проигрыш минимальным, он должен выбирать свой ход из условия:

.

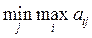Такая стратегия называется минимаксной, а величина β называется верхней ценой игры, или минимаксом.

Цена игры v всегда лежит между нижней ценой игры α и верхней ценой игры β.

.

Существуют игры, для которых нижняя цена игры равна верхней:

.

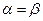Эти игры занимают особое положение в теории игр и называются играми с седловой точкой. Общее обозначение нижней и верхней цены игры:

называется чистой ценой игры.

Седловая точка матрицы – элемент, который минимален в своей строке, но максимален в своём столбце. Это позволяет легко находить седловые точки матрицы.

Точка i =3, j =2, является седловой точкой. Элемент платежной матрицы a₃₂ =4 характеризовался именно тем свойством, что он был максимальным в своём столбце и минимальным в своей строке.

Некоторые вопросы, касающиеся седловых точек.

1. У матрицы быть несколько седловых точек, например у матрицы:

две седловых точки (i =1, j =1) и (i =1, j =3).

2. Не все матрицы имеют седловую точку, например у матрицы седловых точек нет.

Дата добавления: 2014-01-20