Вопрос №3. Электроемкость уединенного проводника. Конденсаторы и их электроемкость. Соединения конденсаторов

Рассмотрим заряженный провод­ник, находящийся так далеко от других тел, что влиянием их электростатических по­лей можно пренебречь. Опыт показывает, что для уединенного заряженного провод­ника, помещенного в сплошной однородный диэлектрик, справедливо соотношение, которое устанавливает пропорциональную зависимость между зарядом q и потенциа­лом φ этого проводника:

1.3

- определение электроемкости проводника

Величина С в выражении (1.3) называется электроемкостью проводника. Со­гласно формуле (1.3). В СИ единица электроемкости — фарад (Ф):

Определим электроемкость С заряженного уединенного проводящего шара ра­диусом R, находящегося в среде с диэлектрической проницаемостью ε. В этом слу­чае: .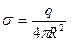

1.4

Из формул (1.3) и (1.4) следует для определения электроемкости С уединенного шара.

1.5

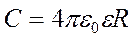
Опыт показывает, что электроемкость С проводящих тел определяется только их геометрическими размерами(формой) и диэлектрической проницаемостью среды, т.е. не зависит от величины заряда.

Задача 1. Определим радиус шара, обладающего электроемкостью С=1Ф, при ε = 1, т.е. в вакууме (ε_о =8,85 · 10^-12 Ф/м):

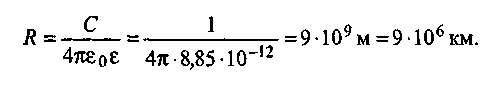
Полученное значение R намного боль­ше радиуса Земли (R₃ ≈ 6,4·10^{-3 км). Это оз­начает, с одной стороны, что С= 1 Ф являет­ся очень большой электроемкостью. В связи с этим широко используются дольные еди­ницы электроемкости (мФ, мкФ, пФ и т.д.). С другой стороны, проведенная оценка по­казывает, что уединенные проводники об­ладают малой емкостью. Поэтому в техни­ческих приложениях используются конден­саторы и батареи конденсаторов, соединен­ных тем или иным способом.}

Два разноименно заряженных проводника определенной геометрической формы при некоторой взаимной ориентации относи­тельно друг друга способны создавать электростатическое поле, которое сосредо­точено (локализовано) в ограниченной об­ласти пространства между этими провод­никами. Такая система двух проводников называется конденсатором, а сами провод­ники — его обкладками. Электроемкость конденсатора:

1.6

Здесь q – заряд одной из обкладок (для определенности положительный);

φ₁ – φ₂ = U — разность потенциалов между обкладками конденсатора, причем поверхности каждой обкладки являются эквипотенциальными.

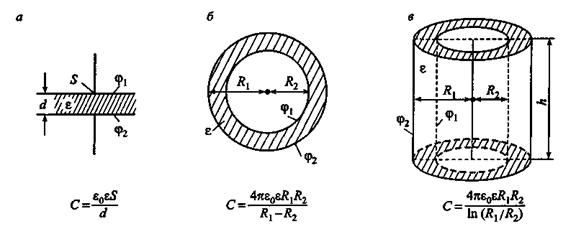
В зависимости от формы обкладок различают плоский, сферический и цилиндри­ческий конденсаторы, емкости которых определяются по формулам, приведенным на рис.3.

	Рис.3

Задача2. Рассчитать емкость плоского конденсатора (рис. 3, а), который состоит из двух параллельных металлических пластин площадью S каж­дая, расположенных на расстоянии d друг от друга и имеющих заряды +q и -q.

Решение:

Если расстояние между пластинами мало по сравнению с их линейными размера­ми, то краевыми эффектами можно пренебречь и поле между обкладками считать однородным. Тогда разность потенциалов Δφ между обкладками φ₁ – φ₂= Ed [φ₁ – φ₂ = σ / εε₀d]. Если между обкладками находится диэлектрик (ε > 1), то поле Е уменьшается в ε раз (Е = σ / εε0), так что для емкости плоского конденсатора(q =σ · S) получим выражение, содержащее только геометриче­ские размеры конденсатора и диэлектрическую проницаемость среды:

	1.7

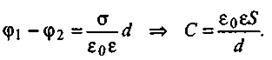
Кроме электроемкости конденсаторы характеризуются пробивным напряжением, которое зависит от свойств диэлектрика, помещенного между обкладками конденсато­ра. В случае необходимости конденсаторы можно соединять в батареи. Электроёмкость батареи из нескольких конденсаторов (i = 1,2, 3…n) определяется по формулам:

1.8

а)

б)

1.9

Формула для параллельного соединения получена из условия, что общий заряд при U_i = U, вторая из условия, что общее напряжение 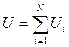(q_i = q).

Дата добавления: 2014-01-20