
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Ранг матрицы. Теорема Кронекера - Капелли
6.1. Ранг матрицы. Вернемся к матрицам. Рассмотрим произвольную матрицу  размера
размера 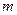 х
х . Ее можно рассмотреть как совокупность
. Ее можно рассмотреть как совокупность 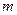 строк длины
строк длины  , т.е. совокупность
, т.е. совокупность 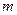 векторов из пространства R n
векторов из пространства R n 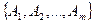 .
.
Определение. Рангом по строкам матрицы  называется ранг системы строк
называется ранг системы строк 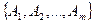 .
.
Обозначение: 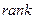
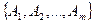 или rг(А).
или rг(А).
С другой стороны, матрицу  можно рассматривать как совокупность
можно рассматривать как совокупность  столбцов высоты
столбцов высоты 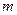 , т.е. множество
, т.е. множество  векторов из пространства R m
векторов из пространства R m 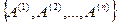 .
.
Определение. Рангом по столбцам матрицы  называется ранг системы столбцов
называется ранг системы столбцов 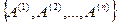 .
.
Обозначение: 
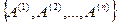 или rв(А).
или rв(А).
Теорема (о ранге матрицы). rг(А)= rв(А).
Прежде, чем доказывать эту теорему, сформулируем и докажем лемму.
Лемма. Элементарные преобразования не меняют ни ранга по строкам, ни ранга по столбцам.
Доказательство. А). Пусть матрица  получена из матрицы
получена из матрицы  применением элементарного преобразования типа I. Равенство rг(
применением элементарного преобразования типа I. Равенство rг( ) = rг(А) очевидно, ведь порядок строк не может влиять на их линейную зависимость. Пусть теперь матрица
) = rг(А) очевидно, ведь порядок строк не может влиять на их линейную зависимость. Пусть теперь матрица  получена из матрицы
получена из матрицы  применением элементарного преобразования типа II:
применением элементарного преобразования типа II: 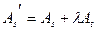 . Ранг по строкам не мог увеличиться: если
. Ранг по строкам не мог увеличиться: если 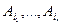 - максимальная линейно независимая система строк, то
- максимальная линейно независимая система строк, то

Тогда

т.е. новая строка  линейно выражается через ту же систему линейно независимых строк. Значит, rг(
линейно выражается через ту же систему линейно независимых строк. Значит, rг( )
) rг(А). Заметим, что обратное преобразование тоже является элементарным преобразованием типа II:
rг(А). Заметим, что обратное преобразование тоже является элементарным преобразованием типа II:  , и поэтому rг(А)
, и поэтому rг(А)  rг(
rг( ). Отсюда rг(
). Отсюда rг( ) = rг(А).
) = rг(А).
Б). Рассмотрим теперь ранг по столбцам. Пусть какая-то система столбцов  была линейно зависимой:
была линейно зависимой:

Числа 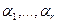 являются решением системы линейных уравнений с матрицей, составленной из столбцов
являются решением системы линейных уравнений с матрицей, составленной из столбцов  . Но элементарные преобразования матрицы не изменяют множества решений системы линейных уравнений, поэтому набор чисел
. Но элементарные преобразования матрицы не изменяют множества решений системы линейных уравнений, поэтому набор чисел 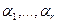 будет решением системы линейных уравнений с матрицей, составленной из столбцов
будет решением системы линейных уравнений с матрицей, составленной из столбцов 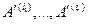 . Это означает, что эти столбцы после преобразования остались линейно зависимыми, и новых линейно независимых систем столбцов не появилось, и rв(
. Это означает, что эти столбцы после преобразования остались линейно зависимыми, и новых линейно независимых систем столбцов не появилось, и rв( )
) rв(А). Но так как обратное преобразование тоже является элементарным преобразованием, то rв(А)
rв(А). Но так как обратное преобразование тоже является элементарным преобразованием, то rв(А)  rв(
rв( ). Значит, rв(
). Значит, rв( ) = rв(А). Лемма доказана.
) = rв(А). Лемма доказана.
Теперь приступим к доказательству теоремы о ранге матрицы.
Доказательство теоремы. Заметим, что, применяя элементарные преобразования, мы можем привести матрицу к ступенчатому виду:
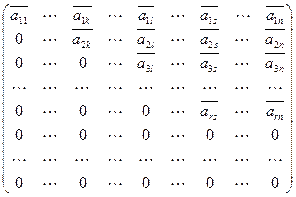 .
.
По лемме rг(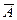 ) = rг(А) и rв(
) = rг(А) и rв(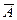 ) = rв(А), поэтому нам достаточно показать, что rг(
) = rв(А), поэтому нам достаточно показать, что rг(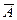 )=rв(
)=rв(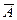 ).
).
Столбцы 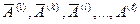 , соответствующие нашим ступенькам (их количество равно
, соответствующие нашим ступенькам (их количество равно  ), линейно независимы. Чтобы это показать, предположим противное: пусть
), линейно независимы. Чтобы это показать, предположим противное: пусть
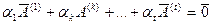 ,т.е.
,т.е.
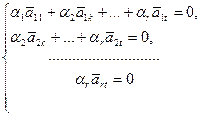
Начиная решать эту систему с последнего уравнения, получаем, что  т.е. линейная комбинация тривиальна. Значит, rв(
т.е. линейная комбинация тривиальна. Значит, rв(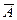 )
) . С другой стороны, столбцы матрицы
. С другой стороны, столбцы матрицы 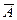 можно считать элементами пространства R r («отрезав» последние
можно считать элементами пространства R r («отрезав» последние  нулевых элементов), следовательно, rв(
нулевых элементов), следовательно, rв(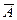 )
) . Значит, rв(
. Значит, rв(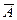 )
) .
.
Разберемся со строками. Строки  линейно независимы, так как равенство
линейно независимы, так как равенство  влечет
влечет
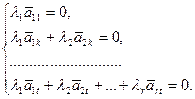
Решая последовательно эту систему уравнений и учитывая, что  , получаем:
, получаем:  Значит, эти строки линейно независимы, и rг(
Значит, эти строки линейно независимы, и rг(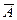 )
) . С другой стороны, множество из
. С другой стороны, множество из  векторов не может иметь ранг больше
векторов не может иметь ранг больше  , поэтому rг(
, поэтому rг(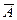 )=
)=  . Итак, rг(
. Итак, rг(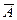 )=rв(
)=rв(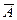 )=
)=  . Теорема доказана.
. Теорема доказана.
6.2. Базисный минор. Ранг матрицы можно вычислить иначе. Напомним, что такое минор матрицы, немного обобщив это понятие. Возьмем не всю матрицу, а только те ее элементы, которые стоят на пересечении некоторых  строк и
строк и  столбцов:
столбцов:
 .
.
Определитель такой матрицы и назовем минором  . Число строк (столбцов) минора назовем порядком минора.
. Число строк (столбцов) минора назовем порядком минора.
Если в матрице есть хотя бы один ненулевой элемент, то существует ненулевой минор порядка 1. Очевидно, что у матрицы размера 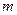 х
х максимальный порядок минора равен
максимальный порядок минора равен  .
.
Пусть у матрицы существует ненулевой минор порядка  и все миноры порядка
и все миноры порядка  равны 0. Такой минор – максимального порядка – назовем базисным.
равны 0. Такой минор – максимального порядка – назовем базисным.
Определение. Базисный минор – ненулевой минор максимального порядка.
Теорема (о базисном миноре). Порядок базисного минора равен рангу матрицы.
Доказательство. 1). Покажем, что если минор 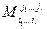 отличен от нуля, то строки
отличен от нуля, то строки 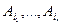 линейно независимы. Допустим противное. Пусть эти строки линейно зависимы, т.е. одна из строк, например,
линейно независимы. Допустим противное. Пусть эти строки линейно зависимы, т.е. одна из строк, например,  линейно выражается через остальные:
линейно выражается через остальные:

Тогда в миноре 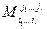 вычтем из последней строки эту линейную комбинацию строк – получим нулевую строку. Пользуясь свойствами определителя, получаем равенство нулю этого минора.
вычтем из последней строки эту линейную комбинацию строк – получим нулевую строку. Пользуясь свойствами определителя, получаем равенство нулю этого минора.
2). Покажем, что если минор 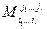 базисный, то все строки матрицы линейно выражаются через
базисный, то все строки матрицы линейно выражаются через 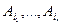 . Составим определитель порядка
. Составим определитель порядка  , добавив к строкам еще одну строку – с номером
, добавив к строкам еще одну строку – с номером  , а к столбцам – еще один столбец – с номером
, а к столбцам – еще один столбец – с номером  :
:

Определитель такой матрицы равен нулю: если  совпадает с одним из номеров
совпадает с одним из номеров 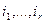 или номер
или номер  совпадает с одним из номеров
совпадает с одним из номеров  ,то мы получаем матрицу с одинаковыми строками или столбцами. Если же ни
,то мы получаем матрицу с одинаковыми строками или столбцами. Если же ни  , ни
, ни  не совпадают с номерами строк или столбцов соответственно, то определитель равен нулю по определению базисного минора.
не совпадают с номерами строк или столбцов соответственно, то определитель равен нулю по определению базисного минора.
Разложим этот определитель по последнему столбцу:
 .
.
Но  - это и есть базисный минор! Значит,
- это и есть базисный минор! Значит,
 .
.
Заметив, что алгебраические дополнения 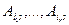 не зависят от
не зависят от  (а только от элементов базисного минора и
(а только от элементов базисного минора и  -й строки), получаем, что
-й строки), получаем, что  -я строка линейно выражается через строки, входящие в базисный минор.
-я строка линейно выражается через строки, входящие в базисный минор.
Подведем итог. Мы получили, что строки, входящие в базисный минор, линейно независимы, а все остальные строки линейно выражаются через них. Значит, эти строки образуют максимальную линейно независимую систему во множестве строк матрицы, и их количество – т.е. порядок базисного минора – равно рангу матрицы. Теорема доказана.
6.3. Теорема Кронекера - Капелли. Система линейных уравнений совместна тогда и только тогда, когда ранг матрицы системы равен рангу расширенной матрицы этой системы.
Доказательство. 1). Пусть дана система уравнений
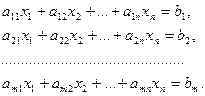
Предположим, что она совместна и набор чисел  - некоторое ее решение. Но тогда
- некоторое ее решение. Но тогда

(напомним,  -
-  -й столбец матрицы). Другими словами, столбец
-й столбец матрицы). Другими словами, столбец 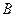 линейно выражается через столбцы исходной матрицы, и, следовательно, ранг системы столбцов
линейно выражается через столбцы исходной матрицы, и, следовательно, ранг системы столбцов  равен рангу системы
равен рангу системы 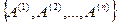 , т.е. ранг матрицы
, т.е. ранг матрицы  равен рангу расширенной матрицы
равен рангу расширенной матрицы 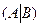 .
.
2).  Пусть известно, что ранг матрицы
Пусть известно, что ранг матрицы  равен рангу расширенной матрицы
равен рангу расширенной матрицы 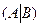 .
.
Тогда максимальная линейно независимая система столбцов матрицы  останется максимальной линейно независимой системой столбцов расширенной матрицы
останется максимальной линейно независимой системой столбцов расширенной матрицы 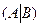 , и столбец
, и столбец 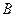 линейно выражается через столбцы матрицы
линейно выражается через столбцы матрицы  :
:
 .
.
Но тогда набор чисел 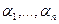 является решением исходной системы, т.е. система совместна. Теорема доказана.
является решением исходной системы, т.е. система совместна. Теорема доказана.
|
Дата добавления: 2014-01-20; Просмотров: 702; Нарушение авторских прав?; Мы поможем в написании вашей работы!