Расчет координат псевдодальномерным методом

Лекция 7 Основы расчета координат потребителя

Обширная теория решения задач пор навигационным определениям изложена в фундаментальной работе коллектива авторов под руководством В. С. Шебшаевича [8]. Серьезные исследования проведены и авторами работы [43].

Аппаратура авиационных пользователей, как правило, ориентирована на выполнение навигационных определений в реальном времени. При этом расчеты производятся при учете всех навигационных спутников, находящихся в поле видимости потребителя.

Достаточно часто в аппаратуре пользователя применяется псевдодальномерный метод. Т.е. определяются псевдодальности до всех видимых навигационных спутников, через которые и вычисляются координаты местоположения.

Сущность псевдодальномерного метода заключается в определении расстояний между навигационными спутниками и потребителем и последующим расчетом координат потребителя. Для расчета трех координат потребителя псевдодальномерным методом необходимо знать расстояния между потребителем и минимум четырьмя навигационными спутниками. Эти расстояния измеряются между фазовыми центрами передающей антенны навигационного спутника и приемной антенны потребителя.

Измеренное расстояние между i-тым навигационным спутником и потребителем называется псевдодальностью до i-го спутника.

Псевдодальность, вообще говоря, также является расчетной величиной и вычисляется как произведение скорости распространения электромагнитных колебаний умножений на время, в течении которого сигнал спутника по трассе «спутник – потребитель» достигнет потребителя. Это время измеряется в аппаратуре потребителя.

Обозначим:

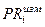- измеренная псевдодальность до i-го навигационного спутника;

Δt_i – время распространения сигнала на трассе «i-тый спутник- потребитель» на момент проведения навигационных определений;

с – скорость распространения электромагнитных волн в пространстве.

Запишем уравнение дальности от потребителя до i-го спутника

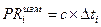. (12.1)

Уравнение (12.1) можно записать через координаты i-го спутника (x_i ,y_i, z_i) и координаты потребителя (x, y, z)

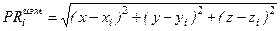, (12.2)

В выражении (12.2) x, y, z – неизвестные, которые требуется определить.

Очевидно, что для решения уравнения (12.2) нужно иметь минимум три уравнения, т.е. рассчитать и определить псевдодальности до трех спутников.

Если это выполнено, то решается система из трех нелинейных уравнений с тремя неизвестными.

Однако в силу того, что шкалы времени навигационных спутников и шкала времени потребителя несинхронизированы при определении псевдодальностей по уравнениям (12.2) появляется погрешность из-за их расхождения.

Поскольку производится одномоментные измерения псевдодальностей, а шкалы времени навигационных спутников синхронизированы между собой, то расхождение шкалы времени спутников и потребителя в момент определения псевдодальностей можно считать величиной постоянной, но неизвестной.

Обозначив эту неизвестную величину через h_t запишем систему уравнений (12.2) в виде

, (12.3)

- погрешность измерения псевдодальности из-за расхождения шкал времени навигационного спутника и аппаратуры потребителя. Для одномоментных измерений эта погрешность одинакова для всех спутников

В системе (12. 3) четыре неизвестных x, y, z, h_t и для ее решения уже необходимо четыре уравнения т.е. требуется определение псевдодальностей минимум до 4-х навигационных спутников.

Результатом решения системы (12. 3) при i = 1,2,…, 4 являются координаты потребителя x, y, z и расхождение шкал времени сети навигационных спутников и аппаратуры потребителя h_t .

Расхождение шкал времени сети навигационных спутников и часов аппаратуры потребителя не является единственным источником ошибок при определении псевдодальностей.

В более общем виде система уравнений (12. 3)может быть записана так

, (12. 4)

где:

Δ_i – погрешности определения псевдодальности до i-го спутника из-за погрешностей предсказания эфемерид, погрешностей частотно-временного обеспечения, погрешностей скорости распространения радиоволн в тропосфере и ионосфере на трассах «i-тый навигационный спутник- потребитель», погрешностей из-за многолучевого распространения сигналов навигационных спутников в месте приема, шумов приемного канала аппаратуры потребителя и погрешностей из-за естественных и преднамеренных помех.

Дата добавления: 2014-01-20