План нахождения наибольшего (наименьшего) значения функции

1. ООФ (если не дан промежуток );
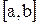2. находим критические точки и смотрим, входят ли они в ;
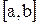3. вычисляем значения функции на концах ООФ (или 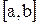) и в критических точках;
4. выбираем среди полученных чисел наибольшее и наименьшее.

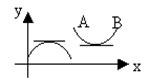
	Дуга АВ, заданная в системе координат, называется вогнутой (выпуклой), если она расположена выше (ниже) касательной, проведенной к этой дуге в любой ее точке.
Точка М дуги АВ называется точкой перегиба, если в ней меняется направление выпуклости данной дуги на вогнутость и наоборот.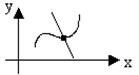

Замечание. Если функция непрерывна на замкнутом промежутке, то по теореме Вейерштрасса она имеет на этом промежутке наименьшее и наибольшее значение. На открытом же промежутке даже ограниченная функция может не иметь наибольшего и наименьшего значения.

Признак монотонности функции

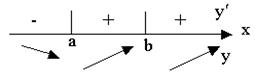
Если на некотором промежутке , то на этом промежутке функция возрастает, если 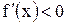, то функция убывает.

Признак функции

Если функция 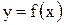непрерывна в точке х=а и в левой ее окрестности (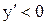), а в

правой - 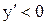(), то в точке х=а функция имеет максимум (минимум).

Признак выпуклости (вогнутости)

Если на некотором промежутке , то на этом промежутке график функции 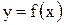является вогнутым (над касательной), если 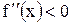- выпуклым (под касательной).

Признак точки перегиба

Если функция 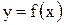непрерывна в точке х=а и в левой ее окрестности 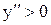(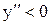), а в правой - 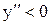(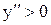), то в точке х=а график функции 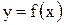имеет перегиб.

ОБЩАЯ СХЕМА ИССЛЕДОВАНИЯ ФУНКЦИИ

1. ОО функции.
2. Четность – нечетность, периодичность. (При наличии четности или нечетности дальнейшее исследование проводится только на половине ООФ: 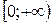или 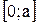; если функция периодична, то ее исследование проводится на промежутке длиною в период).
3. Точки пересечения графика с осями координат .
4. Интервалы знакопостоянства функции.
5. Асимптоты. А) Вертикальная прямая х=а будет асимптотой графика функции 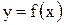, если т. х=а не входит в ООФ и при этом 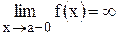или 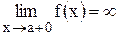. Б) Наклонная прямая 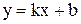будет асимптотой графика функции 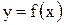на , если 1) 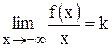(конечное число), 2) (конечное число). Аналогично ищется асимптота на.
6. Интервалы возрастания и убывания, экстремумы функции.
7. Интервалы выпуклости и вогнутости, точки перегиба.

Пример:

Провести полное исследование функции и построить ее график.

Решение:

1) .

2) ,ф-я нечетная и ее график симметричен относительно начала координат. Поэтому далее исследуем функцию только при .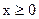

3) Точки пересечения графика с осями координат: х=0 у=0; х=0. Таким образом, М(0;0)- единственная точка пересечения графика с осями координат.

4) Интервалы знакопостоянства: 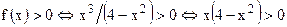, и т.к. рассматриваем только случай 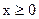, то имеем . Аналогично 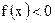при .

5) Асимптоты: 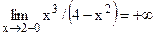, , 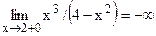т.е. прямая х=2 – вертикальная асимптота. Отсюда, в силу симметрии, следует, что х=-2 - также вертикальная асимптота. Наклонные асимптоты: ,

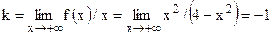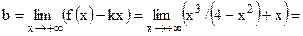
, т.е. – наклонная асимптота. Горизонтальных асимптот график не имеет.

6) Интервалы монотонности и экстремумы: 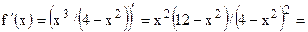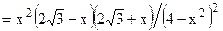. Отсюда видно, что при 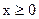(см. рис. 1) функция имеет максимум в точке (причем 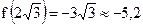), возрастает на (0;2) и 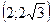и убывает на .

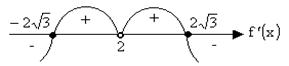
рис.1

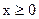7) Интервалы выпуклости и точки перегиба: . Отсюда ясно, что при функция выпуклая (т.е. 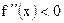) на и вогнута (т.е. 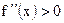) на 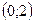, х=0 - точка перегиба.

Учитывая накопленную информацию, строим график функции при 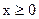, а затем симметрично отражаем его относительно начала координат.

Дата добавления: 2014-01-20