Итеративный метод расчета координат потребителя

Рассмотрим применение псевдодальномерного метода для определения координат потребителя при минимально необходимом и избыточном количестве видимых навигационных спутников.

Псевдодальность до навигационного спутника определяется, как функция

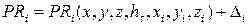. (12. 5)

Зададимся некоторыми априорно известными или заданными координатами потребителя x₀, y₀, z₀, h_t0 и вычислим псевдодальности до всех видимых навигационных спутников:

.

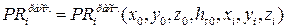Обозначим векторами столбцами искомые координаты потребителя, измеренные псевдодальности и расчетные псевдодальности соответственно

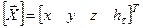, (12. 6)

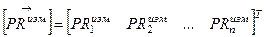, (12. 7)

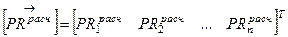. (12. 8)

Образуем из матриц (12. 7) и (12. 8) разностную матрицу

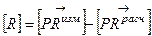. (12. 9)

Запишем (12. 9) с учетом (12. 6)

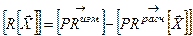. (12. 10)

Допустим, что (12. 9) равно [ 0 ] или почти равно [ 0 ], где [ 0 ] – нулевой вектор столбец..

Разложим матричную функцию 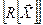в ряд Тейлора в окрестности вектора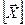

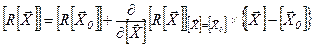. (12. 11)

Запишем, используя (12. 11), матричное уравнение, объединяющее измерения до n навигационных спутников:

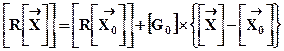, (12. 12)

где:

[G₀] – матрица производных.

Запишем (12. 12) в виде

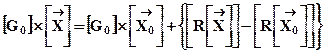, (12. 13)

и разрешим (12. 13) относительно .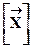

В общем виде матричное уравнение (12. 13) можно решить, если размерность матриц соответствует числу наблюдаемых спутников – n. Для приведения (12. 13) к соответствующей форме умножим левую и правую части (12. 13) на транспонированную матрицу [G₀]^T и на матрицу [W]^-1 = [P]^T´[P], где [P] есть матрица весовых коэффициентов

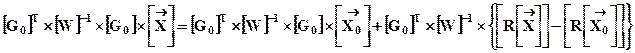. (12. 14)

Решение (12. 14) будет иметь вид:

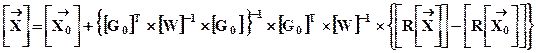.(12. 15)

Матрицы в (12. 15) имеют следующую структуру:

;

;

,

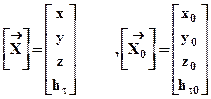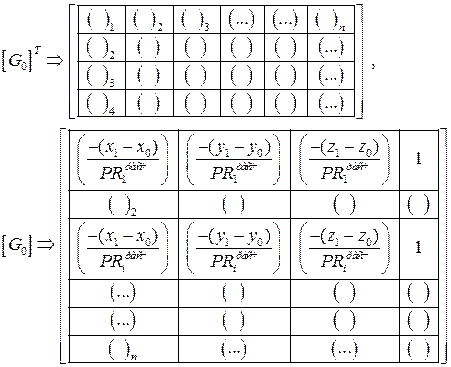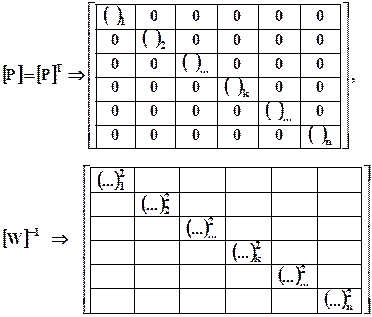где:

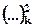- квадрат k – го элемента матрицы [P]

Выражение (12. 15) есть первый шаг метода последовательных приближений. Для определения координат потребителя данным методом необходимо задать начальное приближение вектор 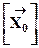, требуемую точность определения координат и погрешности h_t: d_x, d_y, d_z, d_h. При этом выражение (12. 15) записывается в рекуррентном виде:

,

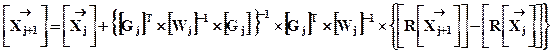(12. 16)

где j изменяется от 0 до K, а K+1 есть число итераций, которое изменяется до тех пор пока не буде выполнено условие:

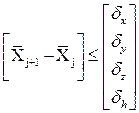. (12. 17)

Отметим, что в соотношениях (12. 11 -12. 16) столбец «i» матрицы [G] вид:

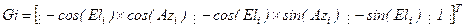, (12. 17)

где:

El_i – угол места i –го спутника (градусы);

Az_i - азимут i –го спутника, измеренный против часовой стрелки от оси «x» (градусы);

i - номер спутника.

Весовые коэффициенты матрицы [W] получают расчетным (экспериментальным) путем или принимаются равными единице.

Дата добавления: 2014-01-20