Многоканальная система с отказами

Рассмотрим классическую задачу Эрланга. Имеется n каналов, на которые поступает поток заявок с интенсивностью λ. Поток обслуживаний каждого канала имеет интенсивность μ. Найти предельные вероятности состояний системы и показатели ее эффективности.

Система S (СМО) имеет следующие состояния (нумеруем их по числу заявок, находящихся в системе): S₁, S₂, …, S_k, …, S_n, где S_k – состояние системы, когда в ней находится k заявок, т.е. занято k каналов.

Для многоканальной (n каналов, на которые поступает поток заявок интенсивности λ, поток обслуживания имеет интенсивность μ) СМО также можно найти предельные вероятности состояний системы и показатели ее эффективности. Система S (СМО) имеет следующие состояния (нумеруем их по числу заявок, находящихся в системе): S₁, S₂, …, S_k, …, S_n. Здесь S_k – состояние системы, когда в ней находится k, т.е. занято k каналов.

Граф состояний СМО, соответствующий процессу гибели и размножения изображен на следующем рисунке:

Поток заявок переводит систему из любого левого состояния в соседнее правое. Интенсивность потока обслуживания, наоборот переводит систему из любого правого состояния в соседнее левое.

Для этой задачи в стационарном режиме Эрлангом были найдены следующие зависимости:

1. Вероятность того, что обслуживания заняты k каналов:

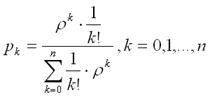(13)

где 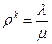, λ – плотность потока заявок;

n – число каналов (приборов),

– параметр обслуживания одним прибором (каналом).

2. Частными случаями (1) будут:

а) вероятность того, что все обслуживающие приборы свободны

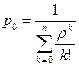; (14)

б) вероятность того, что все приборы заняты. Это одновременно и вероятность отказа в обслуживании вновь поступившего требования в систему:

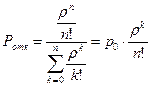. (15)

3. Среднее число приборов, занятых обслуживанием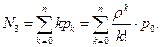

4. Коэффициенты загрузки приборов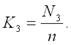

5. Среднее число каналов, свободных от обслуживания .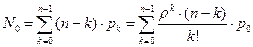

6. Коэффициент простоя каналов: 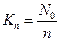. Очевидно N_з+N₀ = n.

Данные формулы Эрланга справедливы для произвольного абсолютно непрерывного закона распределения обслуживания (при условии конечности его математического ожидания).

Пример. Оценить работу АТС, которая имеет n =5 линий связи. Предполагаем, что поток требований простейший с интенсивностью λ = 2 вызова/ед.времени. Продолжительность разговоров распределена экспоненциально, причем 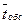= 1 ед. времени.

Решение. Определим коэффициент загрузки ρ = λ / µ = λ ۰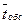= 2. Вероятность того, что все линии связи свободны,

.

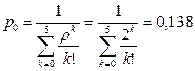Вероятность отказа в обслуживании:

.

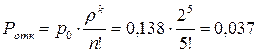Среднее число занятых линий связи:

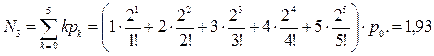линий.

Коэффициент загрузки линий связи:

.

Среднее число свободных линий связи:

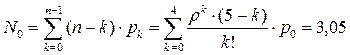
Коэффициент простоя равен:

.

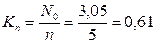Дата добавления: 2014-01-20