Ошибки астатических систем

Если передаточная функция САУ 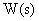обладает астатизмом первого порядка, то в области низких частот 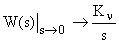. Тогда первая составляющая ошибки определяется как:

.

Следовательно, в астатической системе первого порядка ошибка от задания равного константе равна нулю, ошибка от задания меняющегося с постоянной скоростью равна 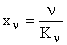, а ошибка от задания, изменяющегося с постоянным ускорением, нарастает до бесконечности.

Если передаточная функция САУ 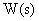обладает астатизмом второго порядка, т.е. в области низких частот . Тогда первая составляющая ошибки:

.

Следовательно, в астатической системе второго порядка ошибки от заданий равного константе и изменяющегося с постоянной скоростью равны нулю, а ошибка от задания, меняющегося с постоянным ускорением, равна константе .

Качество астатических САУ принято характеризовать величинами, называемыми добротностью по скорости и ускорению:

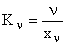и .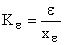

Как показано выше астатические САУ не имеют ошибки от постоянных внешних воздействий. Однако это свойство астатических САУ проявляется далеко не всегда. Проанализируем точностные показатели работы астатической САУ при разных точках приложения внешней помехи. Для этого рассмотрим систему, представленную на рис. 2.

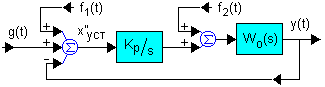
Рис. 2. Астатическая САУ с помехами на входе.

Рассмотрим вторую составляющую ошибки от возмущающих воздействий 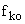. Если САУ астатическая, то , но возможен случай, когда . Т.е. при любой степени астатизма САУ может быть отличной от нуля.

.

Резюме:

Для подавления ошибки от возмущения необходимо, чтобы интегрирующий элемент был включен в контур до места приложения возмущения.

Если рассматривать ошибку чувствительного элемента (сумматора) как возмущение, то, очевидно, что повышение степени астатизма не позволяет устранить ее.

Ошибка при движении по гармоническому закону

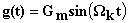
Рассмотрим только первую составляющую ошибки:

где:: 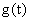— синусоида; — комплексное число

Следовательно:

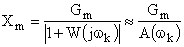
(1)

Резюме:

Формула (1) позволяет идентифицировать положение неизвестной ЛАЧХ на данной частоте по амплитуде ошибки или сформулировать требования к ЛАЧХ при синтезе системы.

Особые точки ЛАЧХ определены комплексными сопряженными корнями. Поведение системы при данных частотах требует дополнительного исследования.

Особенность движения системы при гармоническом сигнале задания — это смена знака координат, которое во многих системах может сопровождаться нелинейными искажениями типа "ступенька" или сменой направления сил сухого трения.

Дата добавления: 2014-01-20