ЛЕКЦИЯ 8. В теории надежности широко используется усеченное нормальное распределение, получаемое из нормального при ограничении интервала возможных значений случайной

В теории надежности широко используется усеченное нормальное распределение, получаемое из нормального при ограничении интервала возможных значений случайной величины х₁, х₂.

Оно в частности, вносит уточнения в расчеты надежности по сравнению с нормальным распределением при больших значениях коэффициента вариации V = s_х / m_x.

Плотность вероятности f(x) усеченного нормального распределения равна ,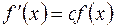

где с – нормирующий множитель, определяемый из условия, что площадь под кривой распределения равна единице

, (2.70)

где , .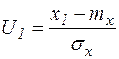

Когда возможные значения случайной величины X лежат в интервале (0,+¥)

.

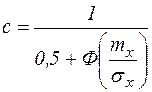Примером усеченных распределений может быть распределение параметра качества изделий после отбраковки части изделий по этому параметру.

В логарифмически нормальном распределении логарифм случайной величины распределяется по нормальному закону. Как распределение положительных величин, оно несколько точнее чем нормальное, описывает наработку до отказа деталей, в частности по усталости деталей (подшипников качения, электронных ламп и др.)

Логарифмически нормальное распределение удобно для случайных величин, представляющих собой произведение значительного числа случайных исходных величин, подобно тому, как нормальное распределение удобно для суммы случайных величин.

При логарифмически-нормальном законе логарифм случайной величины X распределен по нормальному закону.

Плотность вероятности имеет вид

, (2.71)

где М = 0,4343 – коэффициент перехода от натуральных логарифмов к десятичным; s_х – среднее квадратическое отклонение логарифма случайной величины.

Вероятность безотказной работы можно определить по таблицам для нормального распределения в зависимости от значения квантили

.

Например, определить вероятность P (x) отсутствие усталостных повреждений вала в течение t = 10⁴ ч, если ресурс распределен логарифмически нормально с параметрами lg m_x = 4,5; s_х=0,25.

.

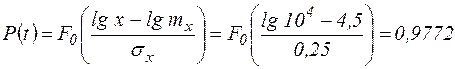Распределение Вейбулла довольно универсально, охватывает путем варьирования параметров широкий диапазон случаев изменения вероятностей.

Вместе с логарифмически нормальным распределением оно удовлетворительно описывают наработку деталей по усталостным разрушениям.

Используется для оценки надежности деталей и узлов автомобилей, тракторов, подъемных машин и всех видов транспортных машин.

Распределение Вейбулла имеет плотность вероятности типа (рис. 2.7)

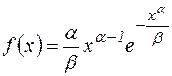, (2.72)

и функцию распределения

. (2.73)

Параметры распределения a и b находятся по формулам

;

.

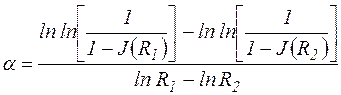Рис. 2.7. Функция (а), плотность (б) и интенсивность (в)

распределения Вейбулла

Правила пользования этими формулами можно уяснить на примере. Данные для расчета следующие:

Длительность испытаний, ч	Количество отказавших элементов, шт	Доля отказавших элементов
		0,26
		0,36
		0,44
		0,57
		0,77
		0,79
		0,87

Проведены испытания партии элементов в количестве

N = 100 шт.

Выбираем границы разбиения R₁ и R₂ опытных данных таким образом, что R₁ < R₂.

Пусть R₁ = 200 ч и R₂ = 2100 ч.

Далее подсчитывается количество элементов n_i, отказавших в диапазонах O – R₁ и O – R₂.

Эти количества равны соответственно O – R₁ = 36

и O – R₂ = 79.

Затем находятся отношения 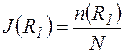; 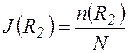, т.е. доля отказавших элементов к моментам времени R₁ и R₂.

В рассматриваемом примере J(R₁) = 0,36; J(R₂) = 0,79.

Значения и 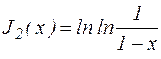находят по таблицам (a = 0,532; b = 37,6).

Дата добавления: 2014-01-20