
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Центрально сжатые элементы
|
|
|
|
Пластические свойства древесины при центральном сжатии проявляются значительно сильнее, чем при растяжении.
Расчет напрочностьдревесины при сжатии выполняется по формуле:
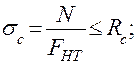
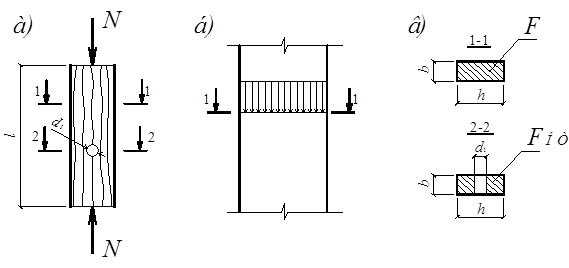
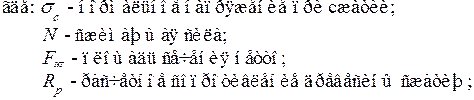
Рис. 8.1. Работа сжатого элемента под нагрузкой.
а) схема сжатого элемента;
б) распределение напряжений в сжатом сечении;
в) площадь поперечного сечения сжатого элемента:
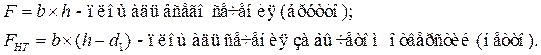 |
Расчет на прочность необходим для коротких стержней или массивных элементов с большими размерами поперечного сечения, для которых выполняется соотношение l ≤ 7 b.
Более длинные и гибкие элементы, рассчитывают на продольный изгиб, который проявляется в потере гибким центрально сжатым прямым стержнем своей прямолинейной формы. Такая форма потери несущей способности называется потерей устойчивости. Потеря устойчивости сопровождается искривлением оси стержня при напряжениях, меньших предела прочности.
Расчет сжатых стержней наустойчивость производится по формуле:
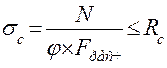
где: φ - коэффициент продольного изгиба;
Fрасч - расчетная площадь поперечного сечения:
если FНТ ≥ 0,75 F, тогда Fрасч = F; если FНТ ≤ 0,75 F, тогда Fрасч = FНТ.
При непрерывном росте сжимающей силы N, наступит момент, при котором стержень потеряет устойчивость. Усилие N, в момент потери устойчивости, называется критическим - Nкр и напряжение в стержне, соответственно, критическим напряжением - σкр.
Физическая суть коэффициента продольного изгиба φ заключается в отношении критического напряжения σкр в сжатом элементе к пределу прочности (временному сопротивлению) материала Rвр:
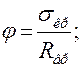
Впервые формулу для наименьшей (устойчивой) критической силы для сжатого стержня из упругого материала в 1757 г. вывел российский математик Леонард Эйлер:
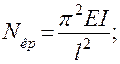
где l – расчетная длина стержня; Е – модуль упругости материала; I – момент инерции поперечного сечения стержня; π – постоянная.
Критическое напряжение σкр, возникающее в стержне при наименьшей критической силе Nкр, не может быть больше временного сопротивления
(в крайнем случае, σкр = Rвр), т.е. коэффициент продольного изгиба может изменяется от 0 до 1.
Критические напряжения σкр равны критической силе Nкр, деленной на площадь поперечного сечения F:
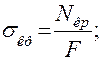
тогда коэффициент продольного изгиба φ:

Корень квадратный из отношения момента инерции I к площади поперечного сечения F, называется радиусом инерции сечения
и обозначается i:
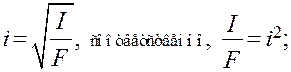
Для прямоугольного сечения наименьший радиус инерции:
i = 0,289× b, где b – ширина сечения стержня (см. рис. 8.1., в).
Чем длиннее стержень и чем меньше размер его сечения, тем более гибким будет стержень. Гибкостью λ называется отношение расчетной длины стержня к радиусу инерции его поперечного сечения:
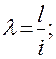 тогда
тогда 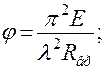
Для идеально упругого материала отношение модуля упругости к временному сопротивлению – величина постоянная. Заменяем все постоянные единым коэффициентом А:
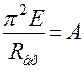 ; тогда
; тогда 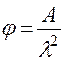 ;
;
Для каждого материала А имеет свое значение. В частности, для древесины А= 3000, для фанеры А= 2500, для полиэфирного стеклопластика А= 1097, для органического стекла А= 580 и т.д.
Долгое время формула Эйлера представляла собой чисто академический интерес. Практическая заинтересованность в вопросах устойчивости стержневых систем появилась в середине XIX века в связи с массовым строительством больших железнодорожных мостов. В 1840 году английский инженер Итон Ходкинсон провел серию экспериментов, которые дали значения критической силы в несколько раз меньше, чем получается из формул Эйлера. Только в конце XIX века выяснилось, что в этих экспериментах потеря устойчивости стержней (довольно коротких и массивных) происходила за пределами пропорциональности, при пластических деформациях, не учитываемых в выводе формулы Эйлера. Таким образом, стала ясной область применимости формулы Эйлера и она в дальнейшем нашла практическое применение.
Для стержней из древесины формула Эйлера действительна при гибкости λ ≥70.
При гибкости λ <70 коэффициент продольного изгиба определяют по эмпирической формуле:
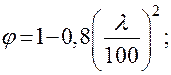
Формула Эйлера была получена путем интегрирования приближенного дифференциального уравнения изогнутой оси стержня при шарнирном закреплении его концов. Эйлер доказал, что потеря устойчивости сжатого стержня происходит в виде искривления оси стержня по синусоиде, причем число полуволн синусоиды зависит от способа закрепления концов стержня. Шарнирное закрепление обоих концов стержня допускает его изгиб при потере устойчивости по одной полуволне синусоиды (рис 8.2., а). Случай шарнирного закрепления стержня считают основным, а остальные случаи приводят к шарнирному при помощи коэффициента расчетной длины μ. Физический смысл коэффициента μ – число полуволн синусоиды, по которой изогнется стержень при потере устойчивости (рис.8.2. б...г).
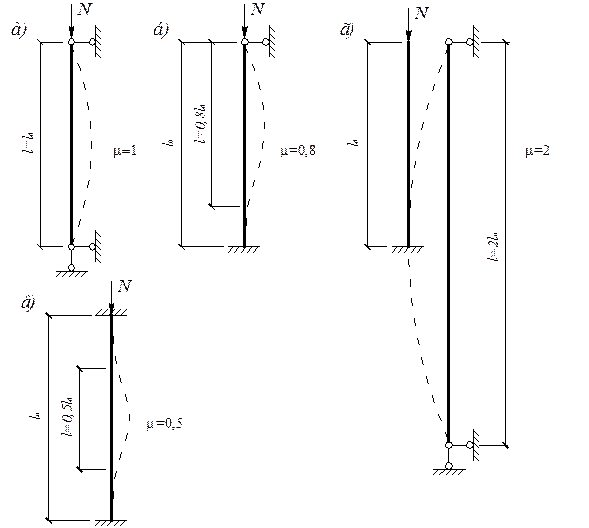
Рис.8.2. Формы потери устойчивости сжатого стержня при различных способах закрепления его концов.
Как уже говорилось выше, гибкость λ напрямую зависит от расчетной длины стержня l. Геометрическая длина стержня l 0 равна фактическому расстоянию между его концами (опорами или узлами). Расчетная длина стержня l равна произведению геометрической длины l 0 на коэффициент расчетной длины μ:
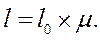
|
|
|
|
Дата добавления: 2014-01-20; Просмотров: 2035; Нарушение авторских прав?; Мы поможем в написании вашей работы!