Изгибаемые элементы

Изгибаемые элементы рассчитывают по первой и второй группе предельных состояний, или иначе, на прочность, устойчивость и жесткость. В расчете по 1 ГПС используют расчетную нагрузку, а при определении прогиба - нормативную (характеристическую) нагрузку, т.е. без учета коэффициентов перегрузки.

Расчет деревянных элементов на изгиб по нормальным напряжениям производят приближенно. При более точном методе потребовался бы учет различных значений модулей упругости в сжатой и растянутой зонах (рис. 8.3.). В сжатой зоне развиваются пластические деформации, которые нарушают прямолинейность распределения нормальных напряжений по высоте сечения (рис. 8.4., б).

Рис.8.3. Относительная приведенная диаграмма работы древесины при растяжении и сжатии (напряжения σ в долях от R_вр, а деформации в %).

1 – при растяжении (модуль упругости Е _р = tg β);

2 – при сжатии (модуль упругости Е _с = tg α).

Нормальные напряжения в изгибаемом элементе определяют при двух допущениях: во-первых, считается, что модули упругости в растянутой и сжатой зонах равны, т.е. Е _р = Е _с, и во-вторых принимается прямолинейное распределение напряжений по высоте элемента, как это показано на рис.8.4., в).

Рис.8.4. Распределение нормальных и касательных напряжений по высоте

поперечного сечения при поперечном изгибе балки.

а) поперечное сечение элемента;

б) фактическая эпюра нормальных напряжений;

в) расчетная эпюра нормальных напряжений;

г) эпюра касательных напряжений.

С учетом этих допущений, прочность по нормальному напряжению в изгибаемых элементах, обеспеченных от потери устойчивости плоской формы деформирования проверяется по формуле:

где: σ_и – нормальное напряжение при изгибе;

М – расчетный изгибающий момент от внешней нагрузки (рис. 8.5.);

W_НТ – момент сопротивления поперечного сечения изгибу нетто; при определении W_НТ ослабления сечений, расположенные на участке длиной
200 мм, совмещаются в одно сечение; момент сопротивления прямоугольного сечения без ослаблений (брутто) определяется по формуле:

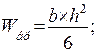
b и h – соответственно, ширина и высота сечения (см. рис. 8.4., а);

R_и – расчетное сопротивление древесины растяжению;

m_б - коэффициент, учитывающий высоту сечения изгибаемого элемента:

Высота сечения h, см	50 и меньше					120 и больше
Коэффициент m б		0,96	0,93	0,9	0,85	0,8

Для промежуточных значений высоты сечения величину коэффициента m_б определяют интерполяцией.

Прочность проверяют в сечении, где действуют наибольшие изгибные напряжения и, дополнительно, в тех сечениях, в которых имеются ослабления.

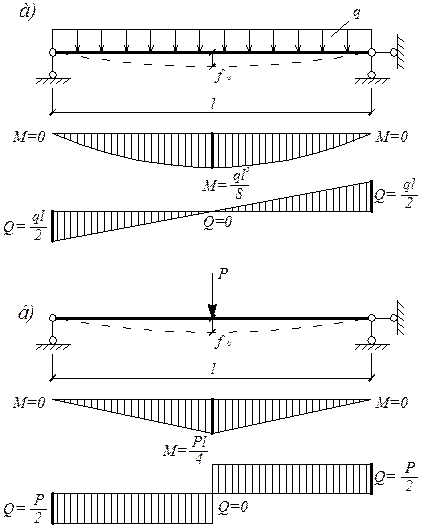
Рис.8.5. Распределение изгибающих моментов М и поперечных сил Q при поперечном изгибе балки.

а) при загружении балки равномерно распределенной нагрузкой, интенсивностью q;

б) при загружении балки сосредоточенной нагрузкой Р посредине пролета.

Кроме нормальных напряжений σ от изгибающего момента М в сечении изгибаемых элементов возникают касательные напряжения τ от поперечной силы Q.

Касательные напряжения определяют по формуле Дмитрия Журавского. Прочность по касательному напряжению проверяют по формуле:

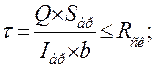
где: τ – касательное напряжение при изгибе;

Q – расчетная поперечная сила от внешней нагрузки (рис. 8.5.);

S_бр – статический момент сдвигаемой части сечения; статический момент прямоугольного сечения изгибаемого элемента определяется по формуле:

І_бр – момент инерции поперечного сечения относительно нейтральной оси; момент инерции прямоугольного сечения изгибаемого элемента определяется по формуле:

b и h – соответственно, ширина и высота сечения (см. рис. 8.4., а);

R_ск – расчетное сопротивление древесины скалыванию.

Касательные напряжения особенно опасны при больших сосредоточенных нагрузках, приложенных вблизи опор, в коротких балках и в балках, имеющих большую высоту сечения (l ≤ 7,8 h), в двутавровых балках.

Помимо расчета на прочность изгибаемые элементы, особенно при их малой ширине, проверяют также на устойчивость плоской формы деформирования:

где: М - максимальный изгибающий момент на рассматриваемом участке l_р;

W_бр – момент сопротивления поперечного сечения брутто;

φ_М – коэффициент устойчивости изгибаемых элементов, шарнирно закрепленных от смещения из плоскости изгиба и закрепленных от поворота в опорных сечениях:

b и h – ширина и высота поперечного сечения элемента;

l_р – расстояние между опорами элемента, а при закреплении сжатой кромки элемента в промежуточных точках от смещения из плоскости изгиба – расстояние между этими точками;

k_ф – коэффициент, зависящий от формы эпюры изгибающих моментов на участке l_р;

k_NM – коэффициент, который вводят при подкреплении из плоскости изгиба в промежуточных точках растянутой кромки элемента на участке l_р; Коэффициенты k_ф и k_NM определяют в соответствии с указаниями
СНиП II-25-80.

Изгибаемые элементы рассчитывают по второй группе предельных состояний, определяя прогиб f ₀ в середине пролета:

1. для шарнирно опертой балки на двух опорах, загруженной равномерно распределенной нормативной нагрузкой qⁿ (рис. 8.5., а):

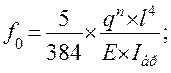
2. для шарнирно опертой балки на двух опорах, загруженной сосредоточенной нормативной нагрузкой Рⁿ в середине пролета (рис. 8.5., б):

где Е – модуль упругости древесины вдоль волокон.

Для элементов из пластмасс, имеющих малый модуль упругости или для деревянных элементов, у которых отношение длины пролета l к высоте поперечного сечения h превышает 15, необходимо учитывать влияние на прогиб касательных напряжений. В этом случае прогиб определяют по формуле:

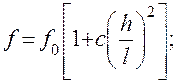
где: f ₀ – прогиб без учета деформаций сдвига;

с – коэффициент, учитывающий влияние деформаций сдвига от поперечной силы, определяется в соответствии с указаниями
СНиП II-25-80.

Относительный прогиб изгибаемого элемента не должны превышать предельного значения, установленного СНиП для каждого вида конструкции:

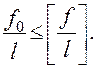
Например, при пролете балок перекрытий и покрытий до 6 м, относительный прогиб не должен превышать 1/200; при пролете свыше 6 м – 1/250; относительный прогиб подкрановых балок – не более 1/400 и т.д.

Дата добавления: 2014-01-20