Проверка значимости коэффициентов. Учет нелинейных членов

Учет нелинейных членов

Принятие решений после построения модели процесса

Интерпретация результатов эксперимента

Проверка адекватности модели

Проверка значимости коэффициентов

Анализ модели начнем с проверки значимости ко­эффициентов. Смысл ее состоит в том, чтобы выяс­нить, равны ли нулю некоторые коэффициенты моде­ли, иными словами, все ли факторы существенно (по сравнению с помехой) влияют на отклик. Для этого не­обходимо сравнить разность между вычисленным зна­чением коэффициента и нулем (или, что то же самое, модуль этого значения) с величиной среднеквадратич­ной ошибки определения этой оценки. Если они одно­го порядка, то факт отличия оценки от нуля можно объяснить помехами, то есть случайными причинами. В этом случае проверяемый коэффициент считается незначимо (несущественно) отличным от нуля и соот­ветствующий фактор удаляется из модели. В противном случае говорят, что он значим, то есть действительно не равен нулю; соответствующий фактор тогда остается в модели.

Формально эта проверка производится следующим образом. Для каждого коэффициента b_i вычисляется отношение

,

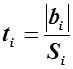где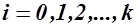

2.Проверка адекватности модели

Следующий этап анализа модели состоит в проверке ее адекватности, то есть проверки того, насколько точно построенная модель описывает проведенный эксперимент. Суть ее состоит в следующем. Оцененную некоторым образом степень рассогласования модели и эксперимента сравнивают с величиной помех в эксперименте. Если они одного порядка, то, очевидно, расхождение между моделью и экспериментом вызвано случайными причинами и модель считается адекватной. В противном случае необходимо признать, что это расхождение не случайно и модель плохо описывает эксперимент, то есть неадекватна.

Степень рассогласования модели и эксперимента оценивается так называемой диспер­сией адекватности S_ад²_.:

Дисперсией адекватности называется остаточная сумма квадратов, т.е. сумма квадратов разно­стей между экспериментальными значениями параметра оптимизации и значениями, предсказанными по уравнению регрессии, деленная на число степеней свободы .

Числом степеней свободы в статистике называется разность между числом опытов N и числом ко­эффициентов (констант), которые уже вычислены по результатам этих опытов независимо друг от друга – (k+1).

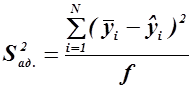
Для проверки гипотезы адекватности используется критерий Фишера F(p, f_восп, f_ад), где f_{восп и} f_ад – степени свободы для дисперсий воспроизводимости и адекватности:

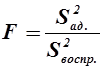
Если F> F_{табл .}, то модель неадекватна, при F≤ F_{т абл} она признается адекватной. Во втором случае правильнее говорить так: у нас нет достаточных оснований, чтобы считать модель неадекватной, или гипотеза об адекват­ности не противоречит опытным данным. Это следует из общих соображений по процедуре проверки гипо­тез. Вероятность признать адекватную модель неадек­ватной не превосходит р.

Дата добавления: 2014-01-20