План решения задач с помощью уравнений Лагранжа второго рода

1. Определить число степеней свободы механической системы и выбрать удобные обобщённые координаты.

2. Вычислить кинетическую энергию системы в её абсолютном движении и выразить её через обобщённые координаты q_j, .

3. Вычислить все производные в левой части уравнений.

4. Определить обобщённые силы Q_j, соответствующие выбранным координатам.

5. Подставить всё в уравнения Лагранжа.

Пример 2.

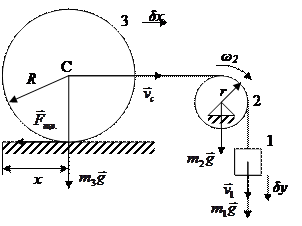Составить дифференциальное уравнение движения механической системы и определить закон движения этой системы при заданных массах тел: m₁, m₂, m₃. Считать, что каток катится без скольжения и пренебречь трением качения.

Решение:

n = j = 1, q = x, 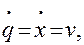v₁ = v_c,

T = T₁ + T₂ + T₃,

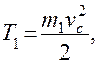
находим производные:

определим обобщённую силу Q, составляя сумму элементарных работ всех сил на возможные перемещения системы:

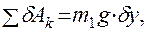δy = δx, Q = m₁g,

подставляем в уравнение Лагранжа:

получали дифференциальное уравнение движения механической системы; для определения закона движения данной системы полученное выражение необходимо дважды проинтегрировать.

Пример 3.

Определить ускорение груза 1, применяя общие уравнения динамики.

Дано: m₁, m₂, m₃.

Решение:

общее уравнение динамики:

зададим системе возможные перемещения:

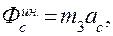
найдём уравнения связи между всеми возможными перемещениями и другие связи между всеми ускорениями; связи между ними точно такие же, как и между соответствующими скоростями:

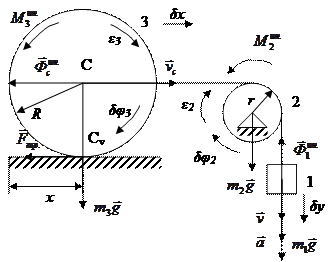
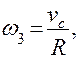v_c = v,

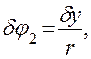
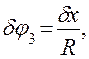δx = δy,

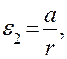
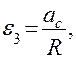a_c = a,

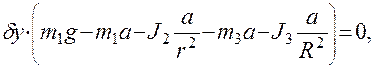δy ≠ 0,

.

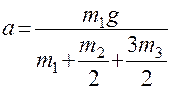Дата добавления: 2014-01-20