Расчет прочности нормальных сечений прямоугольного профиля с двойным армированием (без предварительного напряжения)

Предпосылки расчета прочности нормальных сечений по предельным усилиям. Расчетная схема усилий в нормальном сечении любого симметричного профиля на действие изгибающего момента.

Состояний

Тема: Расчет изгибаемых элементов по I-й группе предельных

Лекция № 9

Вопросы: 1. Предпосылки расчета прочности нормальных сечений по

предельным усилиям.

2. Расчет прочности нормальных сечений прямоугольного

профиля с одиночным армированием на действие

изгибающего момента.

3. То же, с двойным армированием.

4. То же, таврового профиля

Действующие нормы по проектированию железобетонных конструкций допускают применение метода расчета по предельным усилиям для конструкций массового применения. Данный метод является общим для преднапряженных и ненапряженных ж/б элементов и охватывает как случаи изгиба, так и сжатия и растяжения во всем диапазоне эксцентриситетов приложения продольной силы.

Предельные усилия в сечении, нормальном к продольной оси элемента, определяют исходя из следующих предпосылок:

- рассматривается стадия III НДС, т.е. стадия разрушения;

- сопротивление бетона растяжению принимают равным нулю;

- сопротивление бетона сжатию представляется напряжениями, равными R_b и равномерно распределенными по сжатой зоне бетона;

- деформации (напряжения) в арматуре определяют в зависимости от высоты сжатой зоны бетона;

- растягивающие напряжения в арматуре принимают не более расчетного сопротивления растяжению R_s;

- сжимающие напряжения в ненапрягаемой арматуре принимают не более расчетного сопротивления сжатию R_sс;

- напряжения в преднапряженной арматуре, расположенной в сжатой зоне, принимаются равными

(9.1)

где - предельная сжимаемость бетона при осевом сжатии, равная 2×10^-5 при непродолжительном действии нагрузки и 2,5×10^-5 – при продолжительном (т.е. при использовании коэффициента g_b2). В зависимости от величины преднапряжения этой арматуры ее влияние на работу сечения в предельном состоянии будет различным:

1) если к моменту разрушения сечения предварительные растягивающие напряжения 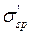будут не погашены (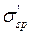>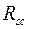), то арматура 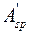будет дополнительно сжимать бетон сжатой зоны - неблагоприятное влияние;

2) если к моменту разрушения сечения предварительные растягивающие напряжения 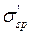будут погашены и по величине 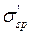<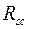, то арматура 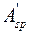будет помогать сжатому бетону – положительное влияние;

3) если к моменту разрушения сечения предварительные растягивающие напряжения 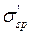будут погашены и по величине 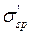=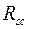, то арматура 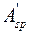не будет оказывать никакого влияния на прочность сечения.

Расчетная схема предельных усилий в нормальном сечении элемента любой симметричной относительно плоскости изгиба формы, соответствующая изложенным выше предпосылкам, приведена на рис. 55.

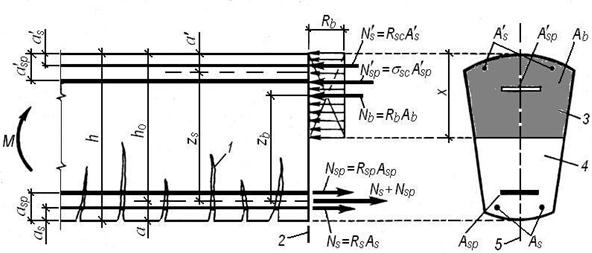
Рис. 55. Схема усилий в нормальном сечении элемента любой симметричной формы:

1 – нормальные трещины; 2 – расчетное нормальное сечение; 3 – сжатая зона сечения;

4 – то же, растянутая; 5 – плоскость изгиба

Расчет по прочности нормальных сечений изгибаемых элементов сводится к решению двух типов задач:

1-й тип – проверка прочности запроектированного (заданного) сечения: по заданным прочностным и деформативным характеристикам материалов, размерам бетонного сечения и площади арматуры определяют минимально возможную (предельную) несущую способность сечения элемента. Несущая способность достаточна, если удовлетворяется неравенство типа

M £ M_u, (9.2)

где M – расчетный (максимально возможный) изгибающий момент в сечении по результатам статического расчета конструкции;

M_u – предельная (минимально возможная) несущая способность сечения при изгибе.

2-й тип – подбор сечений; состоит в том, что из равенства типа

M = M_u (9.3)

определяют размеры бетонного сечения и площадь арматуры; при этом задаются прочностными и деформативными характеристиками материалов и некоторыми из искомых величин (например, размерами бетонного сечения b´h, R_b и R_s).

Рекомендуется проектировать изгибаемые элементы так, чтобы удовлетворялось условие

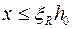, (9.4)

т.е. по 1-му случаю разрушения.

Значение граничной относительной высоты сжатой зоны ξ_R, при котором предельное состояние элемента наступает одновременно с достижением в растянутой арматуре напряжения, равного расчетному сопротивлению R_s (R_sp), определяют по формуле

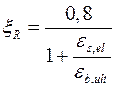, (9.5)

где ε_s,el - относительная деформация растянутой арматуры при напряжениях, равных R_s, определяемая по формулам:

- для арматуры с физическим пределом текучести ; (9.6)

- для арматуры с условным пределом текучести 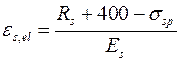, (9.7) где σ_sp - предварительное напряжение в арматуре с учетом всех потерь и коэффициентом точности натяжения γ_sp = 0,9; 400 - в МПа;

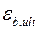- относительная деформация сжатого бетона при напряжениях, равных R_b, принимаемая равной 0,0035.

Замечание. В нормах принято единое обозначение расчетного сопротивления растяжению как для напрягаемой арматуры 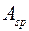, так и для ненапрягаемой 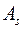; в дальнейшем в тексте тоже будет принято единое обозначение.

В общем случае (рис. 55) в сечении изгибаемого элемента имеется:

- в растянутой зоне – ненапрягаемая арматура 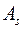с расчетным сопротивлением и напрягаемая арматура 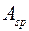со своим расчетным сопротивлением 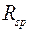(в дальнейшем – тоже обозначается );

- в сжатой зоне – ненапрягаемая 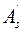с расчетным сопротивлением сжатию 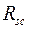и напрягаемая 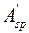с расчетным напряжением .

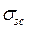Для общего случая предельные усилия в сжатой и растянутой зонах сечения будут равны (см. рис. 55):

в сжатой зоне - 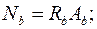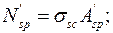(9.8)

в растянутой - 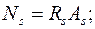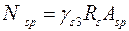. (9.9)

В выражении (9.9) коэффициент 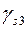³ 1 учитывает то обстоятельство, что к моменту разрушения сжатого бетона фактические напряжения в арматуре с условным пределом текучести могут превышать значение условного предела текучести.

Для решения указанных выше задач при принятых предпосылках достаточно только двух уравнений равновесия статики: и .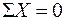

Сумму моментов всех сил обычно принимают относительно оси, проходящей через центр тяжести всей растянутой арматуры А

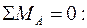
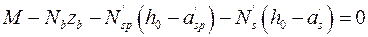; (9.10)

тогда условие прочности (9.2) можно записать в виде

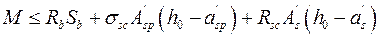, (9.11)

в котором правая часть неравенства есть M_u, т.е. предельная (минимально возможная) несущая способность сечения; здесь 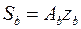- статический момент площади сжатой зоны сечения относительно вышеупомянутой оси.

Высоту сжатой зоны x, входящую в условие (9.11), находят из другого уравнения равновесия – в виде суммы проекций всех сил на продольную ось элемента :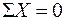

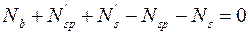, (9.12)

или для сечений, разрушающихся по случаю 1 ():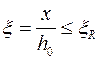

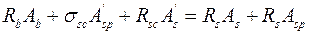. (9.13)

Если в сечении отсутствуют отдельные виды растянутой и/или сжатой арматуры, то в выражениях (9.10)-(9.13) выпадают и соответствующие слагаемые.

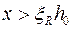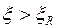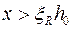Для случая 2-го, отвечающего условию (), когда разрушение происходит по сжатому бетону хрупко, а напряжения в растянутой арматуре не достигают расчетных сопротивлений , высоту сжатой зоны x также определяют из (9.13), заменяя в нем на текущее напряжение . Допускается при определять предельный момент M_u, принимая в выражении (9.13) .

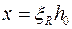2. Расчет прочности нормальных сечений прямоугольного профиля с одиночным армированием (без предварительного напряжения). Если в сжатой зоне арматура отсутствует или не учитывается в расчете (конструктивная арматура), то это будет сечение с одиночным армированием, т.е. арматура имеется только в растянутой зоне. Расчетная схема такого сечения получается из схемы общего случая (см. рис. 55) при исключении из нее соответствующих усилий и приведена на рис. 56.

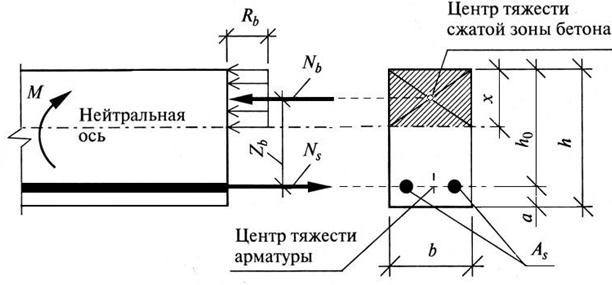
Рис. 56. Расчетная схема для сечения прямоугольного профиля с одиночным армированием

Обозначения на схеме рис. 56:

M – расчетный изгибающий момент от внешних нагрузок (из статического расчета);

b – ширина сечения; как правило, задаются перед расчетом;

h – высота поперечного сечения; предварительно задаются, затем уточняют;

h ₀ = h – a - рабочая (полезная) высота сечения; здесь a = a_b + d /2 – расстояние от центра тяжести всей растянутой арматуры до крайнего волокна растянутой грани сечения; a_b – толщина защитного слоя бетона; d – диаметр рабочей продольной арматуры;

x – высота сжатой зоны бетона;

N_b =R_bbx – равнодействующая сжимающих напряжений в бетоне; R_b – расчетное сопротивление бетона сжатию;

N_s = R_sA_s – равнодействующая растягивающих напряжений в растянутой арматуре; R_s – расчетное сопротивление арматуры растяжению, A_s – площадь сечения рабочей растянутой арматуры;

z_b = h ₀ – 0,5 x - плечо внутренней пары сил.

Для рассматриваемой расчетной схемы можно составить два уравнения равновесия:

1.

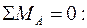
тогда условие прочности (9.2) можно записать следующим образом:

по сжатому бетону: 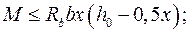(9.14)

по растянутой арматуре: 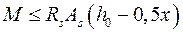. (9.15)

2. :

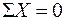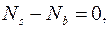
или 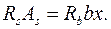(9.16)

Высоту сжатой зоны бетона найдем из (9.16) (9.17)

а относительная высота сжатой зоны

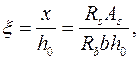(9.18)

или (9.19)

где 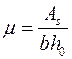- коэффициент армирования сечения.

Для того, чтобы разрушение элемента происходило по случаю 1, т.е. начиналось с растянутой арматуры, должно соблюдаться условие

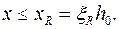
Из (9.19), принимая 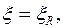можно найти то наибольшее содержание арматуры A_s, при котором сечение еще может разрушаться по случаю 1, т.е. пластично

(9.20)

По формулам (9.14) – (9.18) можно непосредственно выполнить проверку прочности заданного сечения (решить задачу 1-го типа), т.е проверку условия прочности (9.2). Если из (9.16) окажется , то допускается проверку производить также по (9.14), принимая .

Расчетные формулы для подбора требуемой площади сечения растянутой арматуры получают преобразованием выражений (9.14) или (9.15). Подставляя в (9.14) 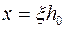, получим

, (9.21)

откуда

(9.22)

или 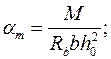(9.23)

здесь 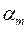- относительный момент усилия N_b сжатого бетона;

; (9.24)

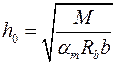. (9.25)

Тогда требуемая площадь растянутой арматуры из (9.16) или (9.18)

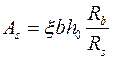. (9.26)

Аналогично преобразуя уравнение (9.15), получим

, (9.27)

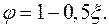(9.28)

Тогда из (9.26)

. (9.29)

Полученные формулы справедливы при

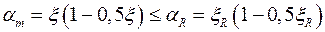. (9.30)

Максимальный момент, который может воспринять сжатый бетон в сечении с одиночной арматурой из (9.23)

(9.31)

Величины 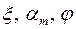взаимосвязаны и могут быть представлены в виде таблицы. Тогда зная одну из них, по табл. определяется любая другая.

Сечениями с двойным армированием называют такие, в которых кроме растянутой арматуры ставят по расчету и сжатую. Необходимость в сжатой арматуре возникает, когда в сечении с одиночным армированием расчетный момент не может быть воспринят лишь бетоном сжатой зоны, т.е. имеет место неравенство

,

или, что то же ,

и возможно разрушение по случаю 2 (хрупкое, по сжатому бетону).

Тогда в помощь сжатому бетону ставят сжатую арматуру. Вообще сечения с двойным армированием неэкономичны по расходу арматуры, поэтому сжатую арматуру ставят по расчету только в следующих случаях:

- при ограниченных размерах поперечного сечения;

- невозможности повышения класса бетона;

- при действии знакопеременных моментов

или других специальных требованиях.

Как отмечалось в лекции №7, сжатая арматура, деформируясь совместно с бетоном, может максимально получить напряжения не более 400…500 МПа, поэтому нецелесообразно применять в качестве сжатой арматуру классов выше А500.

Формулы для расчета нормальных сечений с двойной арматурой получим при предпосылках общего случая и из тех же условий, что и для элементов с одиночной арматурой.

Рис. 57. Расчетная схема для сечения прямоугольного профиля с двойным армированием

В соответствии с расчетной схемой (рис. 57) условие прочности из уравнения равновесия 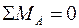имеет вид

,

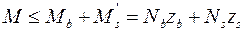или в развернутом виде

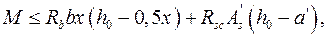(9.32)

или 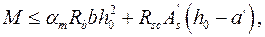(9.33)

где 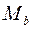- момент, воспринимаемый сжатой зоной бетона и соответствующей (по усилию) частью растянутой арматуры;

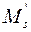- момент, воспринимаемый сжатой арматурой и оставшейся частью растянутой арматуры.

Из уравнения равновесия 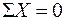имеем

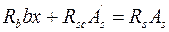, (9.34)

откуда 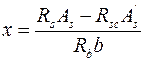. (9.35)

Сечение с двойной арматурой будет наиболее экономичным при максимальном использовании бетона сжатой зоны, т.е. при , или, что то же, при 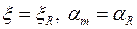. Тогда на сжатую арматуру передается лишь остаток расчетного момента, не воспринимаемый сжатым бетоном

,

или из (9.33) при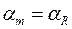

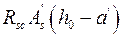=, (9.36)

откуда требуемая площадь сечения сжатой арматуры (в помощь бетону)

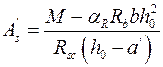, (9.37)

а площадь растянутой арматуры из (9.34) при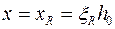

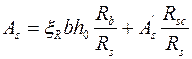. (9.38)

Проверку прочности заданного сечения с двойной арматурой можно выполнить непосредственно по формулам (9.32) и (9.35), которые справедливы при . Когда 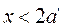, сжатая арматура окажется вблизи нейтральной оси и напряжения в ней будут меньше 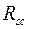. В этом случае, а также при симметричном армировании (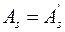) прочность сечения может быть определена без учета бетона сжатой зоны:

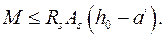(9.39)

Дата добавления: 2014-01-20