Построение разверток развертываемых поверхностей

Развертка поверхностей

Развертка поверхностей.

Лекция № 10

1. Построение разверток развертываемых поверхностей: способом триангуляции, способом раскатки, способом нормального сечения.

2. Построение приближенной развертки неразвертываемых поверхностей.

3. Решение задач.

Разверткой поверхности называется плоская фигура, полученная путем совмещения элементов поверхности с плоскостью.

Если для поверхности можно построить её развертку точно без складок и разрывов, то поверхность называется развертываемой, в противном случае – неразвертываемой.

К развертываемым поверхностям относятся все гранные, а из линейчатых только – цилиндрические, конические и поверхности с ребром возврата.

Существуют следующие способы построения разверток развертываемых поверхностей:

1. Способ триангуляции (треугольников);

2. Способ раскатки;

3. Способ нормального сечения.

Способ триангуляции (треугольников) применяется для построения разверток пирамидальных и конических поверхностей. Они выполняются по одному принципу. Каждая грань пирамиды представляет треугольник и для построения развертки необходимо определить натуральные величины всех сторон треугольника. По найденным натуральным величинам сторон вычерчиваются последовательно треугольные грани. Коническая поверхность, заменяется вписанной в нее, пирамидальной и решение задачи ведется аналогично пирамиде.

Рассмотрим пример, построения развертки, конической поверхности (рис.1)

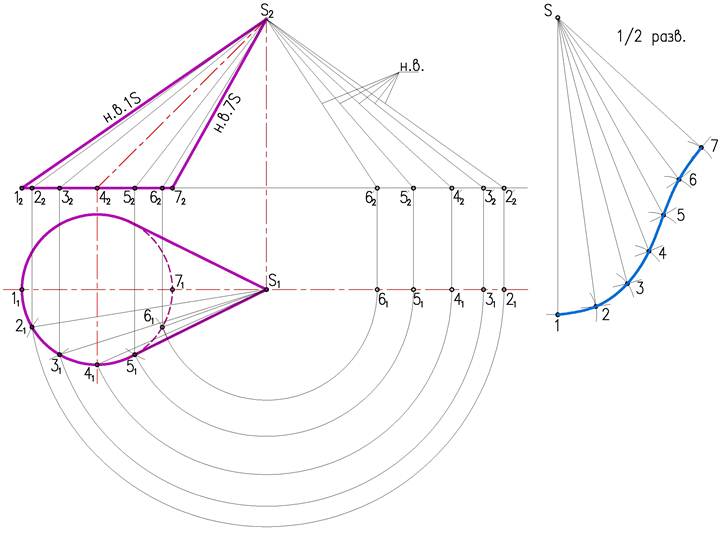Для построения развертки в конус вписываем восьмигранную пирамиду. Т.к. по условию конус расположен симметрично относительно оси, построим половину развертки. Образующие конуса имеют разную длину, поэтому натуральную величину определяем вращением до положения параллельного фронтальной плоскости проекций. Только образующие S₁ и S₅, проецируются в натуральную величину. По полученным натуральным величинам образующих и размерам хорд окружности основания, между образующими, строим половину развертки, состоящую из четырех треугольников вписанной в конус пирамиды. Точки основания соединяем плавной кривой линией.

Способ раскатки применяется для построения разверток призматической и цилиндрической поверхности. И если поверхность цилиндрическая, то в нее вписывается призматическая поверхность. Поэтому принцип построения этих разверток одинаков.

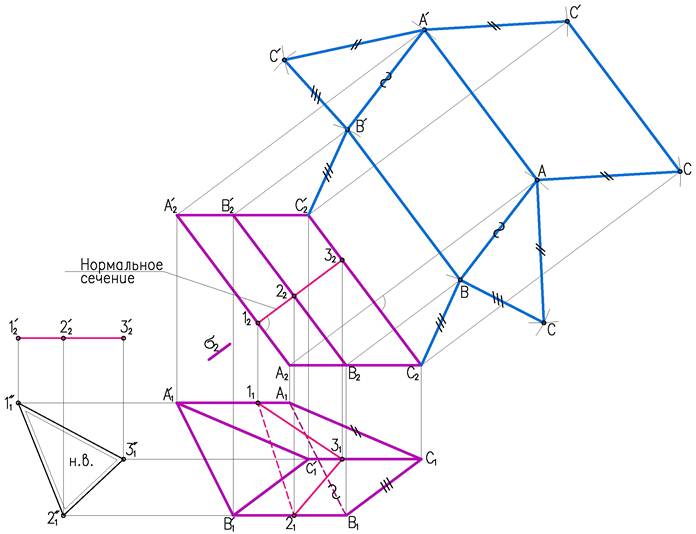
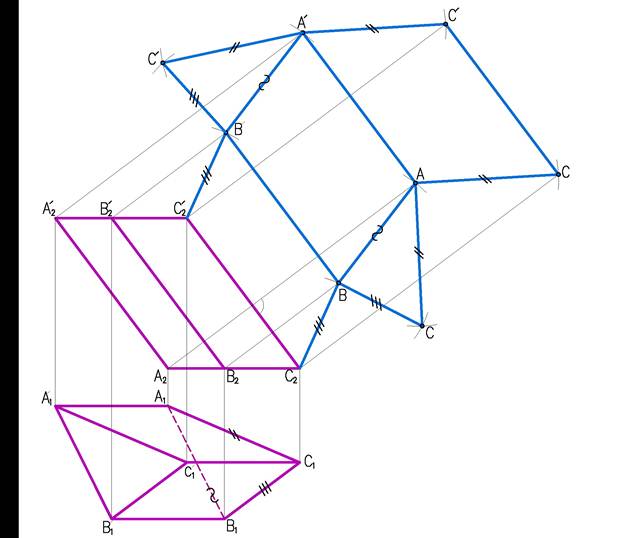Рассмотрим пример построения развертки наклонной треугольной призмы (рис. 2)

Развертку можно выполнять только в том случае, если боковые ребра призмы параллельны плоскости проекций, как на рис. 2. В противном случае сначала, выполняется преобразование (методом замены строим новую проекцию на плоскость параллельную ребрам). При выполнении развертки методом раскатки точки А₂ , В₂, С₂ перемещаются по перпендикулярным к боковым ребрам призмы. А натуральные величины отрезков СВ, ВА, АС берутся из горизонтальной проекции, т.к. основание призмы параллельно плоскости П₁. Боковые ребра остаются на развертке параллельным, т.к. каждая грань призмы является параллелограммом.

Способ нормального сечения используется также, для построения разверток призматической и цилиндрической поверхностей.

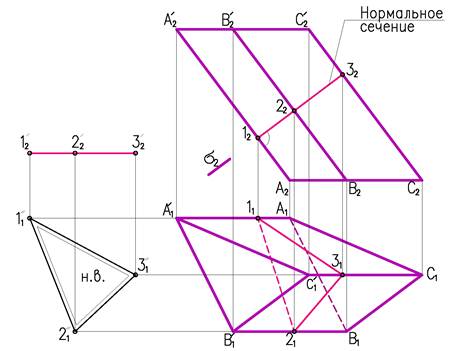
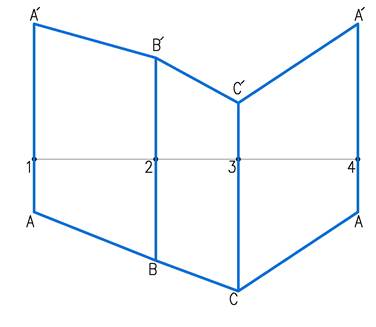
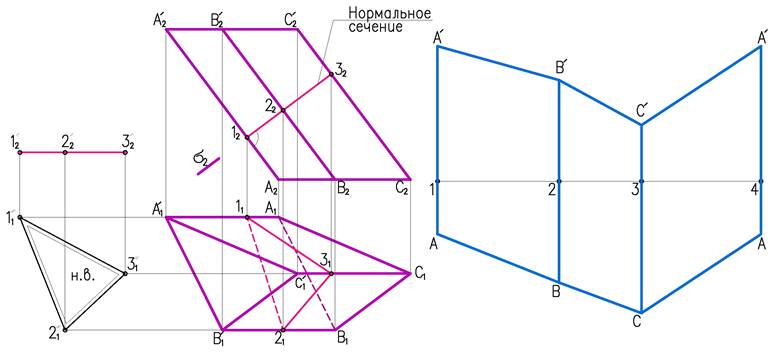
Рассмотрим построение развертки призмы изображенной на рисунке 2. Для этого построим нормальное сечение – сечение перпендикулярное боковым ребрам призмы (∆1,2,3). Определим натуральную величину этого сечения, расположив его параллельно плоскости проекций П₁. Для построения развертки боковой поверхности призмы, строим периметр, треугольника нормального сечения (рис.3). Через точки сечения 1,2,3,1 проводим ребра перпендикулярно сечению и откладываем на них натуральную величину, которая берется из фронтальной проекции рис.2

Дата добавления: 2014-01-20