Частные производные

Эластичность функций нескольких переменных.

Частные производные.

Пусть 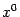- внутренняя точка области 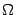, и в области 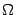задана функция 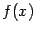. Рассмотрим ограничение функции 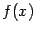на прямую 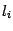, проходящую через точку 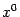параллельно оси . Эта прямая задаётся условиям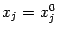и при ; переменная 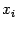может при этом произвольно меняться. Поэтому для рассматриваемого ограничения 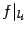имеется естественная параметризация, смысл которой в том, что "замораживаются" все переменные, от которых зависит 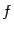, кроме :

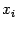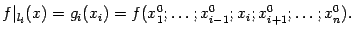
Получили функцию одного переменного , как параметризацию ограничения с помощью параметра .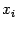

Рис.1.

Функция может иметь производную в точке , равную некоторому числу . Это число называют частной производной функции 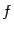по переменной 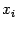, вычисленной в точке 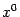. Эта частная производная обозначается 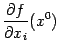или .

Частная производная функции 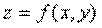по аргументу y является обыкновенной производной функции одной переменной y при фиксированном значении переменной x и обозначается:

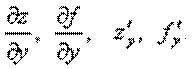
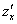или – частная производная по «икс»
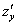или 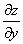– частная производная по «игрек»

1) Когда мы находим частную производную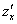,переменнаясчитается константой.

2) Когда мы находим частную производную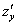,переменная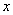считается константой.

Частные производные второго порядка – это частные производные от частных производных первого порядка. Для функции двух переменных вида возможны четыре вида частных производных второго порядка:

Частные производные второго порядка, в которых дифференцирование производится по разным переменным, называют смешанными производными. Смешанные производные второго порядка дважды дифференцируемой функции равны.

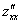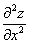или – вторая производная по «икс»

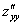или – вторая производная по «игрек»

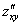или 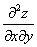– смешанная производная «икс по игрек»

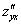или 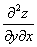– смешанная производная «игрек по икс»

Пример 1

Найти частные производные первого и второго порядка функции

Сначала найдем частные производные первого порядка. Их две.

Обозначения:
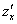или – частная производная по «икс»
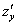или 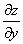– частная производная по «игрек»

Начнем с 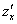. Когда мы находим частную производную по «икс», то переменная считается константой (постоянным числом).

Решаем. На данном уроке я буду приводить полное решение сразу, а комментарии давать ниже.

Теперь 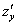. Когда мы находим частную производную по «игрек», то переменная 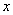считается константой (постоянным числом).

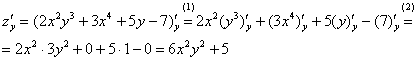
Итак, частные производные первого порядка найдены

Шаг второй. Находим частные производные второго порядка. Их четыре.

Обозначения:
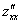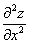или – вторая производная по «икс»
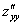или – вторая производная по «игрек»
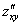или 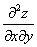– смешанная производная «икс по игрек»
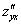или 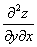– смешанная производная «игрек по икс»

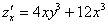
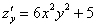
Сначала найдем смешанные производные:

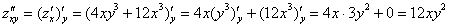
Как видите, всё просто: берем частную производную 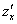и дифференцируем ее еще раз, но в данном случае – уже по «игрек».

Аналогично:

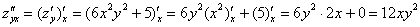
Для практических примеров справедливо следующее равенство:

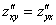
Таким образом, через смешанные производные второго порядка очень удобно проверить, а правильно ли мы нашли частные производные первого порядка.

Находим вторую производную по «икс».
Никаких изобретений, берем 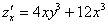и дифференцируем её по «икс» еще раз:

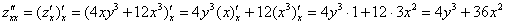
Аналогично:

Пример 2

Найти частные производные первого и второго порядка функции

Геометрический смысл частной производной также становится ясен, если рассмотреть ограничение функции 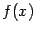, полученное при фиксации значений всех переменных, кроме 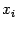. Для наглядности ограничимся случаем функции двух переменных и . В этом случае мы можем изобразить график функции 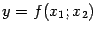на чертеже в виде некоторой поверхности.

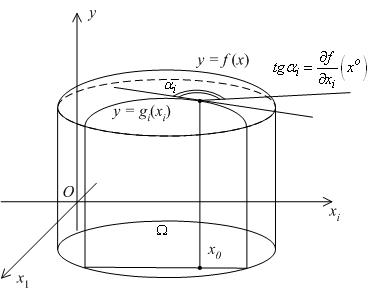
Рис. 2.

Отметим на плоскости 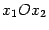точку , в которой вычисляется частная производная 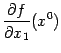, и рассмотрим сечение графика вертикальной плоскостью ; она проходит на плоскости 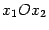через прямую 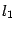, заданную тем же уравнением . Тогда эта плоскость высекает в поверхности графика линию, служащую графиком функции . Функция 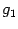-- это функция одной переменной , и её производная в точке равна тангенсу угла наклона касательной, проведённой к графику в точке . С другой стороны, . 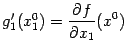Значит, частная производная 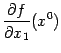имеет геометрический смысл как тангенс угла наклона касательной к сечению графика 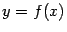вертикальной плоскостью .

Дата добавления: 2014-01-20