Постановка задачи интерполирования

Пусть на промежутке [a,b] задана таблица значений вещественной функции у=f(x):

x	f(x)
a	f(a)
a+h	f(a+h)
a+2h	f(a+2h)
…	…
a+nh=b	f(a+nh)

Требуется найти значение функции в точке 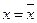, не совпадающей с узлами.

Обозначим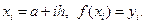

2. Конечные разности

При построении интерполяционного многочлена по равноотстоящим узлам могут быть использованы конечные разности, которые играют роль, подобную той, которую играют производные для функций с непрерывно изменяющимся аргументом.

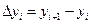— конечная разность первого порядка в точке .

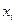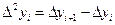— конечная разность второго порядка в точке .

…

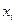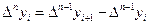— конечная разность n-го порядка в точке .

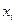Конечные разности можно выразить непосредственно через значения функции:

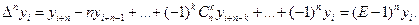
Е — оператор сдвига, так что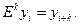

Можно показать, что для достаточно гладкой функции 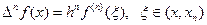и поэтому 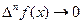при h<1, если 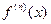не растет очень сильно.

Обратим внимание на очевидное свойство конечной разности: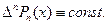

Конечные разности принято записывать в таблицу следующего вида:

x	y	D y	D ^2y	D ^3y
a	y0
		D y0
a+h	y1		D ^2y0
		D y1		D ^3y0
a+2h	y2		D ^2y1
		D y2		...
a+3h	y3		...
		...		...
...	...		...
		Dyn-3		D ^3yn-4
b-2h	yn-2		D ^2yn-3
		D yn-2		D ^3yn-3
b-h	yn-1		D ^2yn-2
		D yn-1
b=a+nh	yn

Таблица 1

Пусть значения функции в узлах интерполирования заданы с точностью e (например, e =1/2*10^-5). Тогда конечные разности имеет смысл вычислять лишь до тех пор, пока они не будут "постоянными" с учетом ошибки округления e в значениях функции, т.е. до тех пор, пока |D^ky_j -D^ky_i|<=2^k+1e — 2^кединиц младшего разряда (объяснить!). Число к<=nпринимаем за степень искомого интерполяционного полинома. Полином будет строиться по (к+1) узлу, которые следует выбирать таким образом, чтобы обеспечить минимальную погрешность (разность между значением функции и значением полинома) в конкретной точке интерполяции 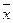: в качестве х₀. выбирается ближайший к 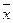узел, х₁ ближайший из оставшихся и т.д. (объяснить используя теорему об остатке интерполирования). В связи с этим рассматриваются три варианта расположения точки интерполирования .

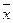Дата добавления: 2014-01-20