Формула Ньютона для интерполирования вперед

Интерполяционный многочлен в форме Ньютона для конца таблицы

Интерполяционный многочлен в форме Ньютона для начала таблицы

Вычисление значения многочлена в точке

Пусть a<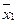<=a+h/2. Узлы следует выбирать в следующем порядке: х₀=а; x₁=a+h; x₂=a+2*h и т. д.

Соответственно используются: y₀, D y₀, D² y₀, D ³y₀ и т.д., отмеченные красным цветом шрифта в таблице 1.

Обозначим t=(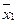-a)/h, тогда

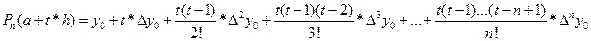
Представим P_n(t) в виде:

где ,...,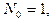

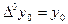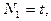Вычисления удобно оформить в виде таблицы 2:

k
D^k y0
Nk(t)
NkD^ky0

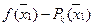
Таблица 2

В ячейки таблицы следует записывать (вставлять формулы в Excel) значения согласно обозначениям, помещенным в первом столбце. В последней строке будут получаться значения многочленов в точке интерполирования нулевой, первой, второй и т.д. степеней. Согласно формуле P_k(t)=P_k-1(t)+N_k(t)D^ky₀, т.е. для к>0 P_k(t) получается сложением значений, находящихся левее по строке и выше по столбцу. Количество цифр после запятой должно быть согласовано с e.

Часто в учебных целях рассматривается модельная задача, т.е. такая, в которой известно аналитическое выражение для интерполируемой функции. В этом случае следует вычислить "точное" значение функции в точке 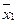, привести его рядом с таблицей, проанализировать результаты.

Пусть b-h/2<=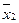<=b. Узлы следует выбирать в следующем порядке: b, b-h, b-2*h и т. д.

Соответственно используются: y_n, D y_n-1, D² y_n-2, D ³y_n-3 и т.д., отмеченные синим цветом шрифта в таблице 1.

Обозначим t=(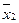-b))/h, тогда

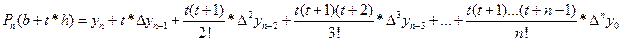
Представим P_n(t) в виде:

где ...,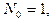

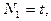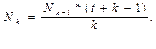
Вычисления следует оформить в виде таблицы, аналогичной таблице 2.

3.3. Интерполяционный многочлен в форме Ньютона-Гаусса для середины таблицы
(интерполирование вперед)

x	y	D y	D ^2y	D ^3y	D ^4y
...
a-3*h	y-3
		D y-3
a-2*h	y-2		D ^2y-3
		D y-2		D ^3y-3
a-h	y-1		D ^2y-2		D ^4y-3
		D y-1		D ^3y-2
a	y0		D ^2y-1		D ^4y-2
		D y0		D ^3y-1
a+h	y1		D ^2y0		D ^4y-1
		D y1		D ^3y0
a+2*h	y2		D ^2y1
		D y2
a+3*h	y3
...

Таблица 3

Пусть а - узел в середине таблицы, т.е. в отличие от предыдущих случаев имеются узлы и левее и правее данного.

Приведем фрагмент таблицы конечных разностей, где y_i=f(a+i*h).

Пусть a<<=a+h/2; Узлы следует выбирать в следующем порядке: а, a+h, a-h,a+2*h, a-2*h и т. д.

Соответственно используются: y₀, D y₀, D²y_-1, D³y_-1 и т.д., отмеченные красным цветом шрифта в таблице 3.

Обозначим t=(-a)/h, тогда:

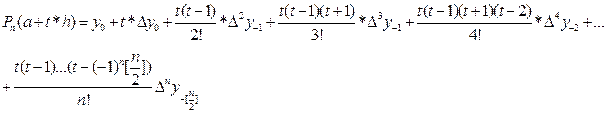
Представим P_n(t) в ви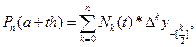де:

где 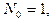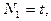и т.д.

Вычисления следует оформить в виде таблицы, аналогичной таблице 2.

Подведение итогов:

Пусть точка интерполирования х находится ближе к левому концу отрезка [a,b] или слева от него. Тогда интерполяционная формула Ньютона для интерполирования вперед примет вид

,

где 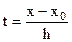- новая переменная, 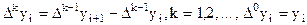- конечная разность k - го порядка.

Дата добавления: 2014-01-20