Лекция 18. Опорожнение водоемов

Опорожнение водоемов.

Очистка водоемов с разработкой донных отложений механизированным способом насухо требует предварительного опорожнения водоема, отвода вновь поступающей воды и проведения первичного осушения донных отложений с нарезкой дренажных траншей.

Одним из существенных вопросов, решаемых при организации работ по очистке водоема, является выбор способа предварительного опорожнения водоема от воды.

На выбор способа опорожнения влияют многие факторы: топографические условия расположения водоема, его геометрические размеры, характер происхождения (природный или искусственный), наличие водосборных сооружений, входящих в состав водохранилищных гидроузлов, глубина воды в водоеме и др.

В практике водохозяйственного строительства известен ряд приемов осушения водоемов. Наиболее просто можно выполнить опорожнение с использованием донного водовыпуска, предусмотренного в составе грунтовой плотины.

При отсутствии или его неисправности, а также при наличии соответствующих условий можно использовать сифонный водовыпуск, устраиваемый на период производства работ.

При невозможности использования сифонного водовыпуска, сброс воды из водоема можно осуществить через проран, устраиваемый в теле плотины или по каналам, отрываемым в грунтовом берегу водоема с отводом воды в пониженные участки рельефа местности.

При отсутствии естественных понижений рельефа местности в близи водоема и сравнительно малом объеме воды в нем, можно применить откачку насосами.

Вопросы для повторения:

1. По каким данным рассчитывается объем донных отложений, и что влияет на величину объема.

2. Процесс саморегенерации в водохранилищах и озерах, их характеристики.

3. Метод определения объема донных отложений.

4. Определение продолжительности производства работ при очистке.

5. Опорожнение водоемов, приемы осушения водоемов перед производством работ.

Краткое содержание: Общее уравнение динамики. Дифференциальные уравнения движения механической системы в обобщенных координатах -уравнения Лагранжа второго рода.
Уравнения Лагранжа в случае потенциальных сил, функция Лагранжа. Выражение кинетической энергии системы через обобщенные скорости и координаты

Общее уравнение динамики (принцип Даламбера-Лагранжа)

Пользуясь принципом Даламбера, можно придать уравнениям движения форму уравнений равновесия, если к активным (заданным) и пассивным (реакции связей) силам присоединить силы инерции.

Пусть имеется СМТ с удерживающими и идеальными связями. Тогда для каждой МТ, входящей в СМТ, согласно принципу Даламбера можно записать:

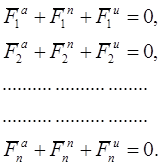(1)

Сообщив МТ, входящим в СМТ, виртуальные перемещения 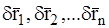, умножим каждое из уравнений (1) на соответствующее 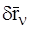, (n=1,2,…,n) и сложим полученные выражения:

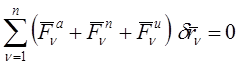. (2)

Так как связи, наложенные на систему, идеальные, то выполняются условия

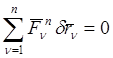(3)

и из (2) получаем общее уравнение динамики

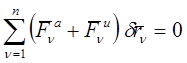. (4)

Общее уравнение динамики утверждает (принцип Даламбера-Лагранжа): При движении механической системы с удерживающими и идеальными связями, сумма элементарных работ всех активных сил, действующих на точки системы и условно приложенных к ним сил инерции на любом виртуальном перемещении равна нулю.

Общее уравнение динамики можно представить также в виде:

(5)

Принцип виртуальных перемещений является частным случаем общего уравнения динамики (в случае равновесия механической системы сила инерции ).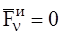

уравнения Лагранжа второго рода (Уравнения движения СМТ в обобщенных координатах)

Используем следующую форму общего уравнения динамики:

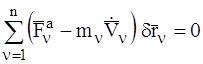. (1)

Пусть на механическую систему, имеющую m степеней свободы, нало­жены голономные, удерживающие и идеальные связи. Введем в рассмотрение m обобщенных координат q_g (g=1,…,m) и выразим через них радиус-вектор n-й точки:

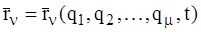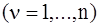, . (2)

Варьируя это соотношение, получим:

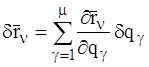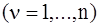, . (3)

Подставляя соотношение (3) в соотношение (1) и изменяя порядок суммирования, имеем:

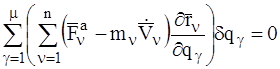. (4)

Так как все 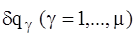независимы и произволь­ны, то равенство (4) может выполняться только тогда, когда каждый из коэффициентов при 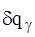равен нулю, поэтому нахо­дим:

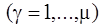. (5)

Эту систему m уравнений запишем в виде:

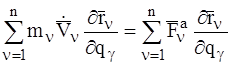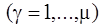. (6)

Правая часть соотношения (6) представляет собой обобщенную силу 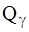соответствующую обобщенной координате :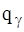

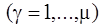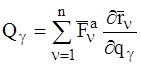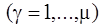. (7)

Преобразуем выражение, входящее в левую часть соотношения (6) следующим образом:

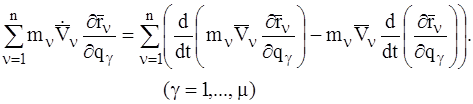(8)

Учитывая, что радиус-вектор n-й МТ зависит от времени t сложным образом, получим из(2)следующее выражение для ее скорости:

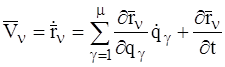, (9)

где 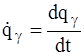– называется обобщенной скоростью (g = 1, 2,…, m).

Так как множители 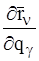(g = 1, 2,…, m) зависят только от обобщенных координат и времени t (и не зависят от обобщенных скоростей), то дифференцируя правую и левую часть соотношения (9) по обобщенной скорости 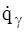, приходим к соотношению:

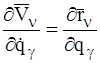. (10)

Найдем частную производную скорости 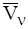по обобщенной координате 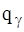, учитывая, что обобщенные координаты входят в правую часть равенства (9) через коэффициенты при обобщенных скоростях:

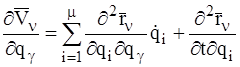. (11)

Частная производная 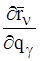зависит от времени t явно и через обобщенные координаты 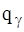, (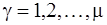). Вычисляя полную производную по времени от частной производной находим:

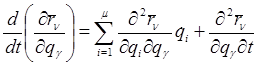. (12)

Сравнивая правые части выражений (11) и (12), замечаем, что

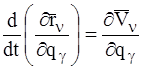. (13)

Возвращаясь к формуле (8) и подставляя в нее тождества (19) и (13), получаем:

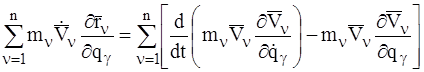. (14)

Учитывая, что

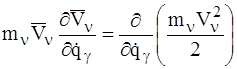и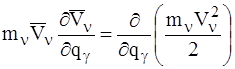

приведем последнее равенство к виду:

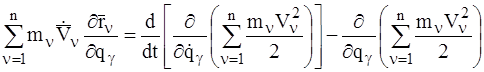. (15)

Кинетическая энергия системы определяется формулой:

,

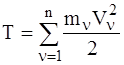тогда (15) примет вид:

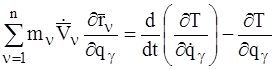
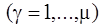. (16)

Подставляя выражения (7) и (16) в уравнения (6), получим:

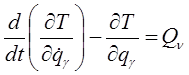
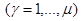. (17)

(17)- уравнения Лагранжа второгорода. Число уравнений Лагранжа второго рода равно числу независимых обобщен­ных координат, т. е. числу степеней свободы этой голономной системы.

Кинетическая энергия системы при подстановке в эти уравнения должна быть предварительно выражена как функция обобщенных скоростей 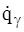и координат 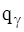. Запишем выражение кинетической энергии механической системы с s степенями свободы, на которую наложены голономные и стационарные связи

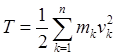
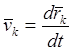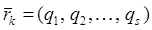Так как и то 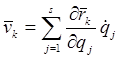и кинетическая энергия является квадратичной формой обобщенных скоростей

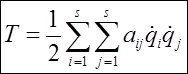
где 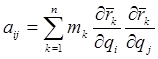— обобщенные коэффициенты инерции, которые в общем случае являются функциями обобщенных координат. Эта квадратичная форма всегда определенно положительна, так как T 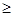0.

Обобщенные силы 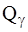тоже могут быть в общем случае функция­ми обобщенных координат 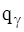, и скоростей 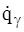. Таким образом, в выражения 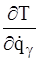, 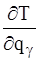и 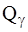могут входить обобщенные координаты 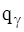и их производные 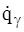. Поэтому в выражение 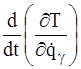войдут уже вторые производные 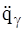. Следовательно, уравнения Лагранжа второго рода (3.18) представляют собой обыкновенные дифференциальные уравнения второго порядка относительно обобщенных координат .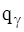

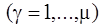Дата добавления: 2014-01-20