Нормальная форма Бойса-Кодда

Определение (надключа). Множество атрибутов, содержащее первичный ключ отношения, называется надключом.

Определение (BCNF). Отношение R находится в BCNF тогда и только тогда, если при наличии в отношении R нетривиальной зависимости x₁,…,x_n ® y, множество атрибутов {x₁,…,x_n} является надключом отношения R.

Детерминантом будем называть атрибут или группу атрибутов, от которой полностью функционально зависит другой атрибут. Например, если имеется зависимость x₁,…,x_n ® y, то множество атрибутов {x₁,…,x_n} называется детерминантом.

Для проверки принадлежности отношения к BCNF необходимо найти все его детерминанты и убедиться в том, что они являются надключами.

Соотношение между 3NF и BCNF. Нормальная форма Бойса-Кодда является усиленной 3-й нормальной формой. Причиной того, что отношение в 3NF не удовлетворяет требованиям BCNF, является наличие нескольких потенциально первичных ключей в отношении.

Схема приведения отношения к BCNF

Рассмотрим отношение R(x₁, x₂, y). Пусть x₁ – первичный ключ, существуют функциональные зависимости x₁ ® x₂, x₁ ® y, а также – зависимости x₂ ® x₁ и x₂ ® y.

a) Предположим, что в отношении отсутствуют повторяющиеся группы атрибутов и, следовательно, отношение R находится в 1NF.

a) Поскольку первичный ключ не является составным, зависимости x₁ ® x₂, x₁ ® y являются полными функциональными зависимостями и, следовательно, отношение R находится в 2NF.

b) Поскольку существует зависимость x₂ ® x₁, зависимости x₁ ® x₂ и x₁ ® y не являются транзитивными. Следовательно, отношение R находится в 3NF.

c) Однако отношение R не удовлетворяет требованию BCNF. Существует, например, зависимость x₂ ® x₁, однако x₂ не является надключом.

Декомпозиция отношения R. L₁={x₁, y}, L₂={x₁, x₂} – подмножества атрибутов.

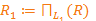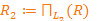, причем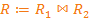

Утверждение. Любое отношение с двумя атрибутами R(x,y) удовлетворяет требованиям BCNF.

Предположим, что в отношении не существует повторяющихся групп записей, и отношение удовлетворяет требованию целостности сущностей (все кортежи уникальны), т.е. рассматривается отношение в 1NF.

Пусть в отношении R не существует зависимостей x ® y и y ® x или существуют одновременно обе зависимости x ® y и y ® x. В качестве первичного ключа выберем пару атрибутов {x,y}.

Если в качестве первичного ключа выбрать, например, атрибут x (при наличии обеих зависимостей), то будут выполнены требования 2NF, 3NF, и не выполнены требования BCNF.

Если в качестве первичного ключа выбрать пару {x,y}, то поскольку неключевых атрибутов нет, выполняются требования 2NF, 3NF, BCNF.

Пусть в отношении R существует зависимость x ® y и не существует обратной y ® x (или наоборот). В качестве первичного ключа выберем атрибут {x}.

Выполняются требования 2NF, поскольку первичный ключ не составной, x ® y является полной, других зависимостей нет.

Выполняются требования 3NF, поскольку в отношении два атрибута, и транзитивных зависимостей нет.

Выполняются требования BCNF, поскольку имеется единственная зависимость x ® y, и атрибут x является надключом.

Выводы

Метод декомпозиции (нормализации) отношения, основанный на анализе существующих зависимостей между атрибутами, позволяет разбить исходную подсхему отношения на две и более подсхем со следующими свойствами:

a) Каждая подсхема отношения удовлетворяет требованиям BCNF, и имеет меньшую степень избыточности информации по сравнению с исходной подсхемой;

b) Исходное отношение может быть восстановлено полностью и без избыточности путем естественного соединения полученных подсхем.

Упражнение 4.

Привести «свой» пример отношения R(x₁, x₂, y) с функциональными зависимостями, рассмотренными при описании схемы приведения отношения к BCNF. В отношении должно быть не менее 6 кортежей. Выполнить декомпозицию отношения на отношения R₁ и R₂ и проверить условие .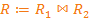

Упражнение 5.

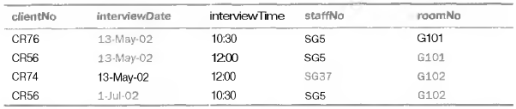
Сотрудники некоторой компании проводят собеседования с клиентами. Информация, относящаяся к этим собеседованиям, приведена в отношении clientInterview. Сотрудникам компании, проводящим собеседования с клиентами, в этот день предоставляется специальное помещение. Однако в течение рабочего дня это помещение может использоваться несколькими разными сотрудниками. С клиентом проводится только одно собеседование в день, но он может участвовать в нескольких собеседованиях в разные дни.

Отношение clientInterview

Покажите, что отношение clientInterview не удовлетворяет требованиям BCNF? Найдите зависимость между атрибутами отношения, детерминант которой не является надключом. Выполните декомпозицию отношения. И проверьте возможность восстановления исходного отношения посредством естественного соединения полученных отношений.

Дата добавления: 2014-01-20