Сущность, назначение и основные элементы статистических графиков

Сущность статистических таблиц и их элементы.

Сущность, назначение и основные элементы статистических графиков.

Понятие, виды статистических графиков и принципы их построения.

1). Графики – условное обозначение числовых величин и их соотношений в виде графических (геометрических) образов – точек, линий, плоскостных фигур, их сочетаний и различного расположения.

Графики служат для облегченного восприятия информации, так как они позволяют с помощью наглядного изображения оценить и осмыслить изучаемое явление.

Классификация графиков

1. По способу построения:

диаграммы:

а) плоскостные (столбиковые, секторные, полосовые);

б) объемные (столбиковые, секторные, полосовые);

в) линейные;

г) фигурные;

д) квадратные;

картограммы (точечные, фоновые);

картодиаграммы (точечные, фоновые).

2. По цели использования:

для характеристики структуры;

для территориального сравнения;

для оценки динамики;

для оценки плановых показателей;

для характеристики вариации;

для оценки взаимосвязей.

Общие правила построения графиков

Для того, чтобы построенные графики наиболее точно передавали реальное состояние явления, необходимо соблюдать следующие правила построения графических изображений.

В зависимости от цели использования необходимо выбрать графический образ (линия, плоскостная фигура и т.д.), который будет наглядно изображать изучаемое явление.

Определить поле графика – пространство, в котором мы разместим геометрические знаки. Поле графика будет характеризоваться размером и своей пропорцией.

Необходимо задать масштабные ориентиры при помощи равномерных или неравномерных шкал масштаба.

Задается система координат для размещения геометрических знаков в поле графика. Чаще всего используется система прямоугольных координат. Данная система изображается с помощью двух осей координат:

ось абсцисс – Х (как правило, горизонтальная линия);

ось ординат – Y (как правило, вертикальная линия).

По оси абсцисс обычно откладывают величину независимой (каузальной, факторной) переменной, а по оси ординат величину зависимой (результирующей) переменной.

Линейные диаграммы служат для изображения статистической величины в виде линий, соединяющих точки, расположенные в поле графика. Служат для характеристики изменения явления во времени, исследования выполнения планового задания, оценки взаимосвязи между явлениями.

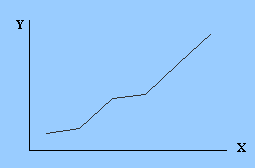
Линейные диаграммы в зависимости от вида функции, описывающей их вид, подразделяются на (см. рис.4.1):

возрастающие и убывающие;

линейные и криволинейные;

возрастающие и убывающие приращения;

огива;

монотонные и немонотонные.

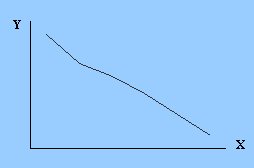
	а) возрастающая функция		б) убывающая функция

Рис. 4.1 Линейные диаграммы

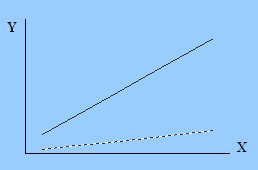
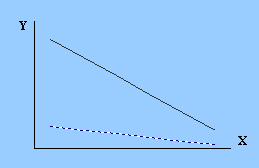
	в) линейные диаграммы с положительным приращением У при различных углах наклона		г) линейные диаграммы с отрицательным приращением У при различных углах наклона
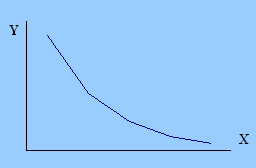
	д) убывающее приращение		е) возрастающее приращение
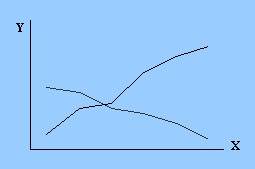
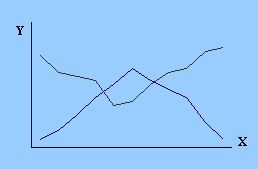
	ж) криволинейные графики, возрастающие и убывающие		з) немоннотонные функции
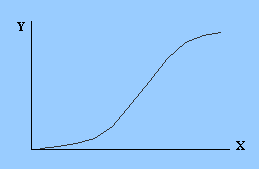
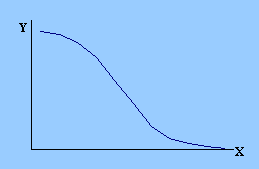
	и) огива (начальный участок - возрастающее приращение ординат, заключительный - убывающее)		к) огива (начальный участок - убывающее приращение ординат, заключительный - возрастающее)
	Рис.4.1. Линейные диаграммы	(окончание)

Возрастающим графиком называется такой график, на котором возрастанию значений на оси X соответствует возрастание значений на оси Y.

Убывающим графиком называется такой график, на котором возрастанию значений на оси Х, соответствует убывание значений на оси Y.

Линейной функция называется, если одинаковым приращениям значения Х всегда соответствуют одинаковые приращения (положительные или отрицательные) значения Y.

Линейные функции отличаются друг от друга углом наклона. Чем больше величина изменения значения Y для данного изменения в величине Х, тем угол наклона будет больше.

Криволинейной функция называется в том случае, если при одинаковых изменениях величины Х, величина Y изменяется неодинаково.

Если при последовательных, равных между собой, одинаковых приращениях значения Х приращения значения Y становятся с каждым разом все больше и больше, то такая кривая называется кривой с возрастающими приращениями.

Если при последовательных, равных между собой, одинаковых приращениях значения Х, приращения значения Y становятся с каждым разом все меньше и меньше, то такая кривая называется кривой с убывающими приращениями.

Исходя из приведенных примеров, можно сказать, что кривые, изображенные на графиках стремятся какого-то придела, верхнего или нижнего, выше или ниже которого значения ординат не поднимутся или не опустятся. Данные пределы или границы, к достижению которых стремятся функции, в статистики получили название асимптоты.

При помощи функций с постоянно возрастающими или убывающими приращениями, а также при помощи линейной функции можно провести интерполяцию и экстраполяцию изучаемого явления, так как определенным изменениям Х, будут соответствовать точно определенные изменения Y.

Интерполяция – нахождение неизвестных промежуточных значений по известным значениям изменяющейся величины с помощью графика.

Экстраполяция – нахождение неизвестных значений, которые или больше или меньше любого значения изменяющейся величины. Экстраполировать – это значит продлить нанесенную на график линию в ту или иную сторону.

S-образная кривая, одни участки которой характеризуются возрастающими значениями прироста ординат, а другие участки – уменьшающимися значениями прироста ординат, в статистике получила название кривой огива.

Если при возрастании значения Х значение Y все время или увеличивается или уменьшается, то такая функция называется монотонной функцией. Все приведенные выше примеры являются примерами монотонных функций.

Если при возрастании значения Х, значение Y в некоторых интервалах увеличивается, а некоторых уменьшается, то такая функция называется немонотонной функцией.

Плоскостные и объемные диаграммы

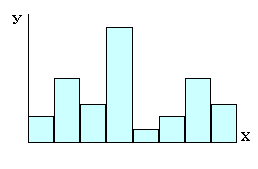
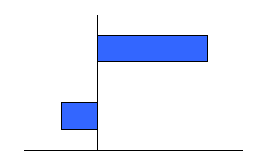
Столбиковые диаграммы используются при изучении динамики изучаемых явлений, для характеристики вариации в рядах распределения, для сравнения и так далее.

Столбиковые диаграммы часто применяют для изучения структуры явлений. В этом случае каждый столбик (явление) разделен на части, пропорциональные удельному весу отдельных частей целого.

На данной диаграмме два столбика (два явления) разделены пропорционально удельному весу отдельных частей, из которых состоит явление.

Секторная диаграмма – круговая или полукруговая диаграмма, подразделенная на секторы пропорционально удельному весу отдельных частей целого (таким образом круговая диаграмма является диаграммой структурной). Размерность долевой структуры целого выражается угловой величиной каждого сектора.

Если:

диаграмма круговая то 100% – 3600, соответственно 1% – 3,60

диаграмма полукруговая 100% – 1800, соответственно 1%–1.80

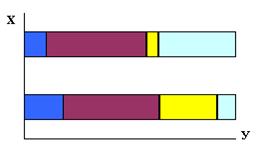
Полосовая диаграмма является разновидностью столбиковой диаграммы. Различие полосовой диаграммы от столбиковой диаграммы заключается в горизонтальном расположении столбиков (полос) одинаковой ширины, но разной длины, пропорциональной изображаемым величинам. Особенно удобна полосовая диаграмма в случаях, когда отдельные объекты сравнения характеризуются противоположными по знаку показателями.

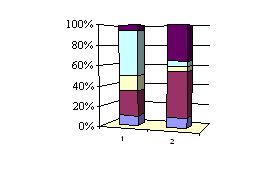
	а) столбиковая диаграмма плоскостная		б) диаграмма столбиковая, структурная, объемная
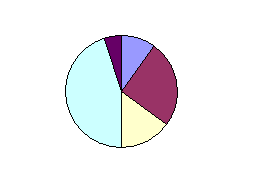
	в) диаграмма круговая		г) полосовая диаграмма
	д) структурная полосовая диаграмма		е) диаграмма фигурная
	Рис.4.2. Плоскостные и объемные диаграммы

Для изучения структуры явления используются полосовые диаграммы удельных весов.

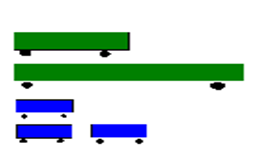
Данная диаграмма вычерчивается в виде определенного количества каких либо фигур (обычно это упрошенное изображение объектов изображаемого явления). Фигурная диаграмма строится двумя методами:

сравниваемые величины изображаются фигурами различных размеров;

сравниваемые величины изображаются разной численностью фигур одинакового размера.

Если сравниваемые объекты имеют резко отличные значение показателей, то их сопоставление с помощью столбиковой диаграммы практически невозможно. В этом случае применяются квадратные или круговые диаграммы.

Квадратная диаграмма изображает величины явлений, выраженные площадями квадратов стороны, которых пропорциональны квадратному корню числовых размеров изучаемых явлений.

Статистические карты. Картограммы, картодиаграммы

Статистические карты используются для изучения географического распространения явления. Основными видами статистических карт являются картограммы и картодиаграммы.

Картограммы служат для графической характеристики пространственного распространения явления. Виды картограмм:

1. Фоновые картограммы – это картограммы, на которых различия в величине изучаемого явления, в разных районах изучаемой территории, выражаются насыщенностью (интенсивностью фона). В монохромных картограммах степень интенсивности фона определяется густотой штриховки, в цветных – интенсивностью окраски (причем необходимо использовать оттенки только одного цвета).

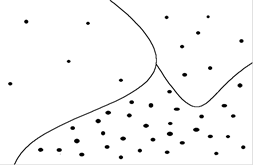
2. Точечная картограмма это картограмма, на которой величина изучаемого явления показывается числом точек в данном районе.

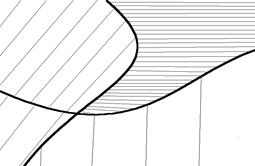
Картодиограммы – это географическая карта, совмещенная со статистическими диаграммами (столбиковыми, круговыми, секторными и т.д.). Картограммы и картодиограммы строятся с помощью изолиний. Изолинии – это кривые линии, ограничивающие на географической карте территории с одинаковыми размерами статистического признака (количество трудовых ресурсов, средняя температура, качество почвы и так далее) (см. рис. 4.3).

	а) картограмма фоновая штриховая		б) картограмма фоновая цветная
	в) картограмма фоновая точечная		г) картодиаграмма
	Рис. 4.3. Картограммы, картодиаграммы

Дата добавления: 2014-01-20