УЭ 5.2-3. Выбор режима работы

При работе в широких диапазонах значений частот (или перио­да сигнала) естественно возникает вопрос, какой режим (из двух рассмотренных) целесообразно выбрать для минимизации отно­сительной погрешности результата измерения. Рассмотрим этот вопрос на основе сравнения функций суммарных погрешностей в обоих режимах.

На рис. 6.10, а приведен график функции суммарной относи­тельной погрешности в режиме измерения частоты f_x.

В целях упрощения рисунка симметричный по отношению к оси абсцисс график здесь представлен модулем (только положи­тельной частью). Для правомерного сравнения погрешностей в обоих режимах необходимо их представить зависимостями от общего аргу­мента, например, от измеряемой частоты f_x. Поскольку период Т_х сигнала есть обратная частоте f_x величина:

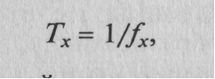
то выражение для суммарной относительной погрешности δ_T, %, результата измерения периода Т_х можно представить так:

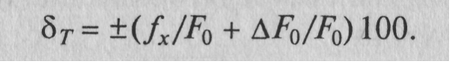
Графически эта зависимость показана (своим модулем) на рис. 6.10, б.

Теперь, имея зависимости суммарных погрешностей (δ_F и δ_T), %, обоих режимов от одного и того же аргумента (измеряемой частоты f_x):

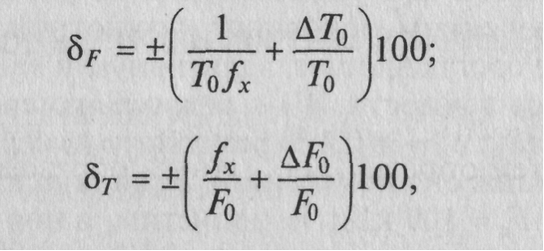
можно сравнивать их значения при конкретной измеряемой часто­те и, следовательно, выбирать оптимальный режим. Поведение от­носительных суммарных погрешностей в зависимости от значения измеряемой частоты f_x в обоих режимах показано на рисунке 5.12, в.

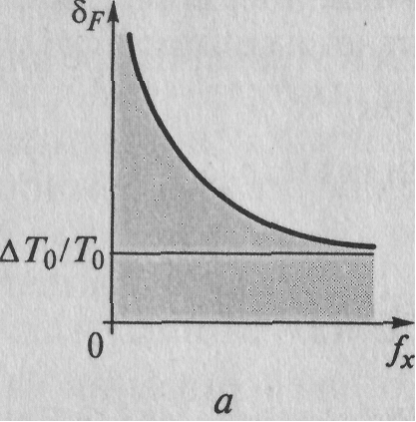
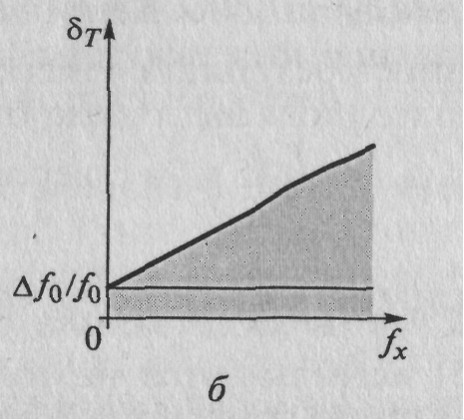
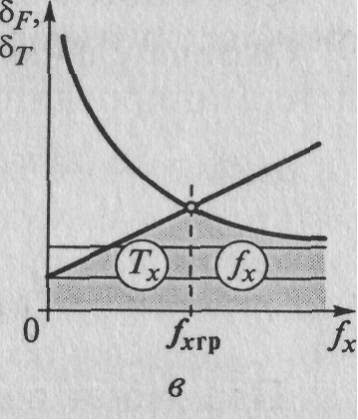
Рисунок 5.12. К вопросу выбора режима ЦЧ:

a — δ_F (f_x) врежиме изменения частоты; б — δ_T (f_x) в режиме изменения периода; в — сравнение относительных суммарных погрешностей

Точка пересечения графиков суммарных погрешностей на рисунке 5.12, в означает равенство относительных погрешностей изме­рения δ_F = δ_T,что соответствует граничному значению измеряемой частоты f_xгр. Для обеспечения минимальных погрешностей резуль­татов при измерении частот, меньших f_xгр, следует использовать режим измерения периода Т_х, а для частот, больших f_xгр — режим измерения частоты f_x.

Обычно в структуре ЦЧ для формирования интервала Т₀ ис­пользуется тот же генератор тактовых импульсов, что и при зада­нии образцовой тактовой частоты F₀. Поэтому относительные от­клонения ΔТ₀/Т₀ и ΔF₀/F₀ равны, т.е. относительные погрешности задания интервала Т₀ и образцовой частоты F₀ одинаковы. Следо­вательно, сравнение суммарных относительных погрешностей мо­жет выполняться без учета этих мультипликативных составляю­щих. В результате можно определять значение граничной частоты f_xгр простым выражением

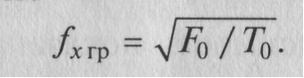
Если значение входной измеряемой частоты больше значения f_xгр, то целесообразно выбрать режим измерения частоты f_x, если меньше — то, наоборот, режим измерения периода Т_х.

Классы точности ЦЧ задаются (как и у большинства ЦИП) предельным значением основной абсолютной погрешности Δ _п, содержащей две составляющие: аддитивную и мультипликативную. Например, класс точности ЦЧ в режиме измерения частоты мо­жет быть задан так: Δ _п = ±(0,1 % результата измерения + 0,1 % верх­ней границы диапазона измерения). Если диапазон измерения ча­стоты известен F_K = 100 кГц, и, допустим, в нормальных условиях проведения эксперимента получен результат измерения частоты f_x = 50 кГц, то можно найти значение основной абсолютной инст­рументальной погрешности результата:

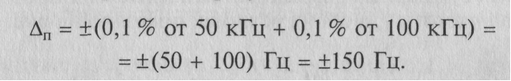
Окончательная запись результата измерения в этом примере для детерминированного подхода выглядела бы так:

Дата добавления: 2014-01-20