Лекция №11. Степень устойчивости и степень колебательности линейных систем регулирования

Степень устойчивости и степень колебательности линейных систем регулирования

Нахождение системы для практических целей на границе устойчивости не обеспечивает работоспособность систем.

Любое даже небольшое внешнее или внутреннее возмущение способно вывести ее из устойчивого состояния.

Это связано с тем, что нахождение вектора разомкнутой системы вблизи опасной точки не гарантирует перехода в область неустойчивого равновесия. Значит, система должна обладать запасом устойчивости.

Запас устойчивости систем, по модулю и фазе. Показатель колебательности М.

Если динамические свойства системы заданы КЧХ, то удобно оценивать запас устойчивости системы непосредственно по удалению КЧХ от опасной точки(-1; i 0).

В этом случае оценка запасов устойчивости определяется по двум величинам: запас устойчивости по модулю-С; запас устойчивости по фазе –φ.

Запасом устойчивости по модулю называют длину отрезка С, равного расстоянию от точки пересечения КЧХ разомкнутой системы до опасной точки(-1; i 0).

Данное число показывает, на сколько должен измениться модуль КЧХ разомкнутой системы при неизменных фазовых соотношениях, чтобы система вышла на границу устойчивости.

Запасом устойчивости по фазе называют угол, который лежит между вещественной отрицательной полуоси, проведенным из начала координат в точку пересечения КЧХ с окружностью единичного радиуса и с центром в начале координат.

Численно запас устойчивости по фазе показывает, на сколько должно увеличиться отставание по фазе в разомкнутой системе при неизменном модуле: чтобы система вышла на границу устойчивости.

Для работоспособной системы необходимо, чтобы она обладала некоторым запасом устойчивости как по модулю, так и по фазе.

Степень удаления КЧХ разомкнутой системы от опасной точки можно определить так же по величине максимума АЧХ замкнутой системы.

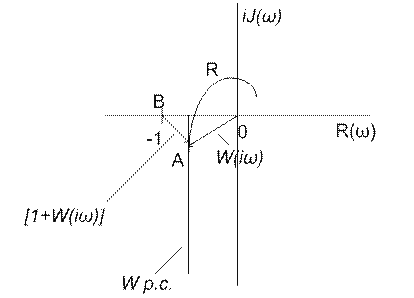
Предположим W(iω)=

Рассмотрим замкнутую систему: для замкнутой системы

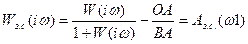
при частоте ω1.

Если КЧХ проходит далеко от точки (-1; i 0), то длина отрезка ВА все время будет больше отрезка ОА и при стремлении ω→∞; ВА→1, а длина ОА→0

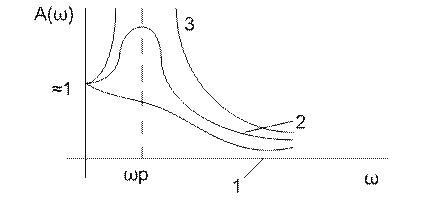
1. далеко от (-1; i 0)

2. близкое соседство

3. проходит через точку(-1; i 0)

При достаточно близком соседстве с опасной точкой длина отрезка ВА может оказаться меньше отрезка ОА на некоторых низких частотах, которые назовем ω=ωр.

ωр- резонансная частота, наблюдается минимум амплитуды, которая на других частотах снижается.

Будем считать, что КЧХ проходит непосредственно через опасную точку, тогда для АЧХ замкнутой системы на этой частоте уходит в бесконечность.

Вывод: чем больше максимальное АЧХ замкнутой системы, тем ближе КЧХ разомкнутой системы к точке (-1; i 0)- это означает уменьшение запаса устойчивости.

Отношение- это максимум АЧХ замкнутой системы.

Данное отношение при проектировании может задаваться, регулируя т.О запас устойчивости

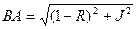
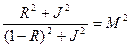
После преобразования данного соотношения относительно параметра R будем иметь следующую характеристику

Данное соотношение является уравнением окружности с радиусом

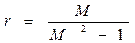
Центр данного радиуса расположен на отрицательной вещественной полуоси на расстоянии

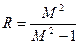
М- это показатель колебательности

Изобразим семейство окружностей для различных значений М

Круговая диаграмма

В практическом случае по этой характеристической диаграмме можно настроить АЧХ замкнутой системы, если на неё нанести КЧХ разомкнутой системы.

Значения амплитуды замкнутой системы при некоторой частоте равно индексу М-окружности, которая пересекает разомкнутую характеристику на этой частоте. Максимум амплитуды в этом случае будет равен точке касания.

Обычно величиной М можно задаваться при проектировании систем. Величина М находится в пределах 1,1…1,6, что обеспечивает достаточно высокий запас устойчивости.

Особенности динамических характеристик в промышленных объектах.

Реальные промышленные объекты по своим свойствам значительно сложнее, чем типовые динамичные звенья и, по сути, представляют совокупность различных элементарных звеньев, в тех или иных вариантах соединений.

1свойство, которое следует учитывать, является сложность описания и представления объектов в виде их динамических звеньев.

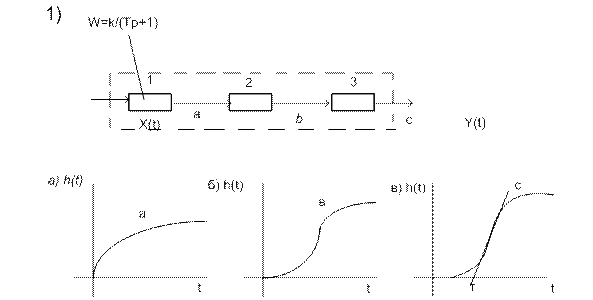
I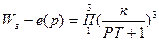

II

2 свойство: промышленные объекты могут кроме сложного математического описания описываться уравнениями частных производных. Это говорит о том, что системы обладают специфическими свойствами, которые учитываются производными.

3 свойство: практически во всех промышленных объектах имеются запаздывание; говорит о том, что преобразование в объекте и его представлении на выходе запаздывает относительно входа

На КЧХ это отображается улиткообразной характеристикой

Дата добавления: 2014-01-20