История психиатрической помощи

Классификация сил, действующих в жидкости

При изучении механики твердого тела обычно рассматривают две категории сил – сосредоточенные и распределенные. В жидкости, как правило, необходимо исследовать действие только распределенных сил, так как приложение к ней сосредоточенных сил обусловливает появление разрывов в жидкости.

Для классификации сил, действующих в жидкости, применим известный из курса сопротивления материалов метод сечений: выделим в движущейся жидкости произвольный жидкий объем V, ограниченный поверхностью S (рис. 2.1), и мысленно отбросим всю жидкость вне этого объема.

При этом внутренние силы, действующие между выделенной и отброшенной частями жидкости, перейдут в категорию внешних сил, распределенных по поверхности S. Таким образом, влияние отброшенной жидкости проявляется в виде поверхностных сил, приложенных к поверхности раздела S.

Кроме них, в любой точке объема V действуют массовые силы, пропорциональные массе жидкости, заключенной в элементарном объеме ∆V, окружающем данную точку (рис. 2.1). Рассмотрим более подробно эти две категории сил.

Массовыми называются силы, приложенные к каждой частице жидкости и пропорциональные ее массе. Обозначим через ∆f массовую силу, приложенную к жидкой частице с массой ρ ∆V, и введем понятие напряжения массовой силы, характеризуемого в данной точке вектором F, определяемым как предел отношения вектора массовой силы к массе частицы:

. (2.1)

Если вектор F постоянный, то напряжение массовых сил равно отношению массовой силы, действующей на объем, к массе этого объема.

Напряжение массовых сил имеет размерность ускорения [F] = LT^-2.

Составляющие вектора F на оси декартовых координат обозначим F_x, F_y, F_z. В общем случае F является функцией радиуса-вектора точки r и времени t; F = F (r, t).

К массовым силам относятся, например, силы тяжести, силы инерции и электромагнитные силы.

Определим вектор напряжения массовых сил в наиболее важном частном случае действия силы тяжести. Вес элементарной частицы

∆Р = ρ ∆Vg.

При выборе направления оси z вверх массовая сила 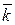, где
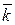= орт оси z.

Получаем что

F = –kg (2.2)

Или

F_x = 0; F_y =0; F= – g. (2.3)

В ряде практически важных случаев массовые силы потенциальны. Обозначим через U потенциал напряжения массовых сил.

При этом вектор их напряжения F можно определить как градиент скалярной функции U:

(2.4)

или

(2.5)

В случае, когда массовой силой является сила тяжести, согласно (2.3) и (2.5):

,

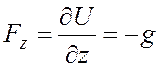откуда следует, что

U = – gz+C. (2.6)

Произвольную постоянную С можно отбросить, так как ее величина не влияет на определение вектора F.

Таким образом, потенциал силы тяжести определяется выражением:

U = –gz. (2.7).

Поверхностными называются силы, распределенные по поверхно­сти S, ограничивающей выделенный объем жидкости (рис. 2.2).

Это неверное определение!!!

Обозначим через ∆р_п поверхностную силу, приложенную к площадке ∆S с внешней нормалью п. В общем случае ∆р_n действует под углом к внешней нормали. Введем понятие вектора напряжения поверхностных сил в данной точке поверхности, определяя его как предел отношения:

. (2.8)

Из (2.8) следует, что вектор напряжения поверхностных сил представляет отношение поверхностной силы к величине элементарной площадки. Следовательно, р_п имеет размерность L^-1 MT^-2.

В общем случае р_п не является обычным вектором. Его величина в данной точке зависит от ориентации площадки, выделенной внутри объема жидкости. Иными словами, если через данную точку провести одинаковые по величине, но различные по ориентации площадки, то действующие на них векторы р_п напряжения поверхностных сил будут различны. Поэтому в общем случае р_п зависит от радиуса-вектора точки, ориентации площадки и времени:

. (2.9)

Физическая величина, характеризуемая в данной точке вектором р, принимающим бесчисленное множество значений в зависимости от ориентации площадки, называется тензорной.

Одной из важнейших задач гидромеханики является определение гидродинамических реакций, действующих со стороны жидкости на тело. Когда поверхность S в жидкости совпадает с поверхностью твердого тела, то это свидетельствует, что к ней со стороны жидкости приложены напряжения р_п. Следовательно, элементарная сила воздействия dR со стороны жидкости на площадку поверхности тела dS определится выражением:

dR = p_ndS,

а элементарный момент относительно начала координат:

,

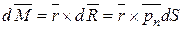где r – радиус-вектор центра площадки.

Интегрируя dR и dM по поверхности S тела, получим общие формулы для результирующей R и момента М гидродинамических сил, действующих на тело:

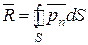; (2.10)

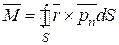. (2.11)

Для использования общих выражений (2.10) и (2.11) требуется отыскать зависимости напряжений р_п от скорости течения жидкости, формы тела и физических свойств жидкости. Исследование этих зависимостей и явится одной из главных задач курса.

Подчеркнем, что массовые силы, действующие в жидкости, влияют на гидродинамические реакции, возникающие на теле, лишь через напряжения поверхностных сил.

Термин «психиатрия» ввел в обращение Й. Рейль в 1803 году, с тех пор в течение 200 лет происходят непрерывное накопление и систематизация данных в области психопатологии. Слово «психиатрия» (от лат. «psyche» - душа, «iatros» - врач) означает врачевание психиатрических расстройств, компетентную и умелую помощь душевно больным людям, а также всякому человеку нуждающемуся в такой помощи.

С именем Ф. Пинеля связано создание основ научной психиатрии. Он освободил психически больных от оков, уничтожив так называемый синдром цепей, что позволило изучать проявления психозов в естественных условиях. Именно Пинель разработал простую и удобную классификацию психозов, впервые выделив «манию без бреда» (психопатия) и определив судебно-психиатрическую оценку этих больных. На склоне лет он стал академиком и консультантом императорского двора Наполеона.

В медицине античности — периода, который охватывает промежуток от V в. до н.э. вплоть до V в. н.э., — психиатрии как самостоятельной науки еще не существовало, но проявления душевных заболеваний уже были в то время известны. Эти расстройства с интересом изучали врачи того времени, многие из которых также были знаменитыми философами своей эпохи (Эмпедокл, Аристотель, Теофраст, Демокрит и др.).

Высокую степень развития обнаруживает психиатрия в сочинениях Гиппократа. По его мнению, душевные болезни объясняются исключительно телесными причинами и заболеваниями мозга. Гиппократ и его последователи различали главным образом две основные формы помешательства: «меланхолию» и «манию». Эти наименования, как полагают многие историки медицины, были известны еще до Гиппократа и сохранились до настоящего времени. Под «меланхолией» (в переводе с греч. — черная желчь) понимали все формы помешательства, происходящие от избытка черной желчи, в том числе и сумасшествие в самом прямом смысле. «Мания» (в переводе с греч. — неистовствовать, предугадывать, прорицать) обозначала сумасшествие вообще. Гиппократ впервые разработал номенклатуру бредовых состояний. Он среди них выделял такие, как «парафронейн» (бред вообще), «паракронейн» (галлюцинирование, сильная степень бреда), «паралерейн» (бред, бессвязная речь), «паралегейн» (заговаривание, меньшая степень бреда); эти типы упоминаются в гиппократовском сборнике «Эпидемии». Особой заслугой Гиппократа является расшифровка сущности «священной болезни», или эпилепсии. Он писал: «Относительно болезни, называемой священною, дело обстоит таким образом: насколько мне кажется, она не божественнее, не более священна, чем другие, но имеет ту же природу происхождения, как и прочие болезни».

Медики, философы, историки времен античности обращали пристальное внимание на острые проявления безумия. В этом смысле особенно интересны высказывания Геродота, современника Гиппократа, родоначальника исторической науки, который описывал случаи психического заболевания (именно слово «заболевание» он использовал в своей книге) у спартанского царя Клеомена: «Спартанский царь Клеомен после утомительного путешествия вернулся в Спарту и заболел помешательством. Впрочем, он и раньше не совсем был в здравом уме — каждый раз при встрече с кем-нибудь из спартанцев он бросал им в лицо палку. Ввиду такого поведения родственники посадили Клеомена в колодки, как помешанного. Находясь в заключении, он заметил однажды, что страж при нем остался один и потребовал у него меч: тот сначала отказался, но Клеомен стал угрожать ему наказанием впоследствии, и под страхом угроз страж подал ему меч. Взявши меч в руки, царь стал изрезывать себя в полосы, начиная с бедер, а именно он резал на себе кожу в длину от бедер до живота и поясницы, пока не дошел до желудка, который тоже изрезал в узкие полоски, и так умер». Причину такого помешательства, по Геродоту, называли сами спартанцы, которые прекрасно знали все обстоятельства жизни царя: при каждом приеме иностранных послов и по всякому поводу вообще он неумеренно пил неразбавленное вино, так что Клеомен заболел от пьянства. Отсюда видно, что древние эллины отмечали силу внешних (экзогенных), в частности алкогольных, факторов, могущих вызвать помешательство.

Гиппократ и приверженцы его школы рассматривали ряд болезненных состояний психики как особые болезни.

Психиатрические взгляды Сократа отражены достаточно ясно в работе его ученика Ксенофонта, посвященной памяти незабвенного учителя. Безумие, по мнению Сократа, составляет противоположность мудрости. Здесь он рассуждал, как Пифагор, который различал два понятия: «дианойя», нормальное состояние психики, противопоставлялась «паранойе» — безумию. Сократ не считал безумием незнание. Но если кто не знает самого себя (старая греческая мудрость — «познай себя») или составляет себе мнение о том, чего не понимает, то это, как полагал Сократ, граничит с безумием.

Если обобщить сказанное в отношении медицины античности, можно сделать вывод, что шло постепенное уточнение признаков различных душевных заболеваний, утверждалась терминология, которая впоследствии определяла психиатрическую лексику (мания, меланхолия, френит, паранойя, истерия, эпилепсия, ипохондрия, характеры), при том что специального выделения душевных болезней в нозологическом смысле еще не было. Это был препарадигмальный, донозологический период, досистематический этап формирования психиатрии.

Дата добавления: 2014-01-20