ЛЕКЦИЯ 7. Момент силы относительно точки и оси

Момент силы относительно точки и оси.

Пары сил и действия с ними.

Вопросы лекции.

1. Момент силы относительно центра.

2. Момент силы относительно оси.

3. Понятие пары сил. Момент пары. Действия с парами сил.

1. Момент силы относительно центра.

Сила – количественная мера механического взаимодействия. Однако, в некоторых случаях она не совсем удобна для характеристики взаимодействия. К этому пришли в результате изучения поведения рычагов и вращения твёрдых тел.

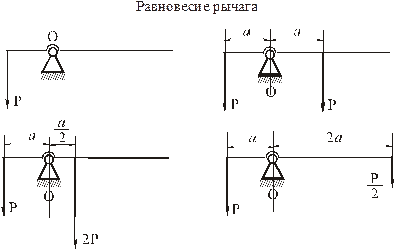
Поэтому пришли к необходимости ввести ещё одну меру механического взаимодействия – момент силы.

Моментом силы относительно центра О называется вектор, равный векторному произведению радиус-вектора точки приложения силы на вектор силы.

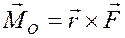
По определению векторного произведения

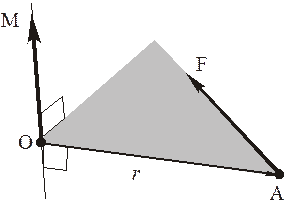
т.е. 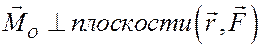, и направлен так, что с конца вектора момента вращение происходит против хода часовой стрелки.

Модуль момента силы определяется по формуле

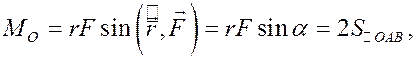
где точка В – конец вектора силы,

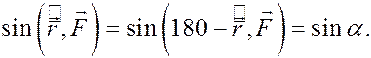
Учитывая, что

где h – длина перпендикуляра, опущенного из точки О на линию действия силы, формулу для модуля момента моно представить в виде

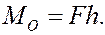
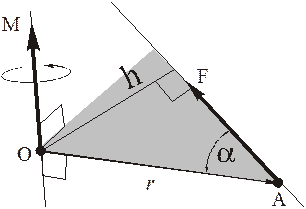
Величину h называют плечом силы относительно точки.

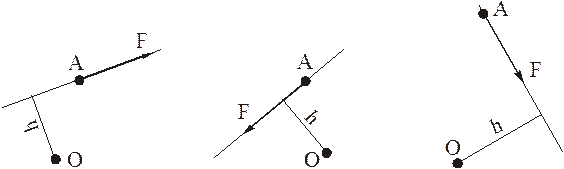
Различные направления вектора момента силы показаны на рисунках.

На следующих рисунках показаны плечи сил относительно центров.

Если вектор силы задан проекциями 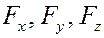на оси координат, а точка её приложения – координатами ,

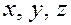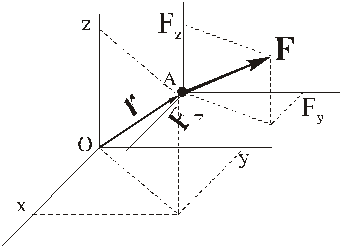
то вектор момента силы может быть вычислен аналитически:

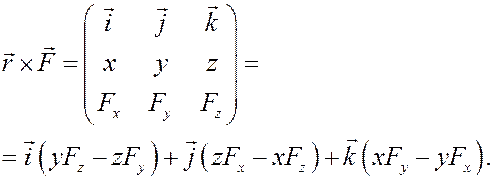
Сравнивая с аналитическим представлением любого вектора

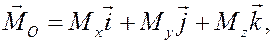
для проекций вектора момента получаем равенства

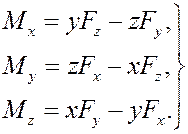
Тогда модуль момента будет

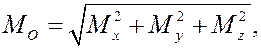
а направляющие косинусы –

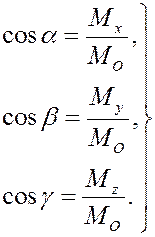
Система сил 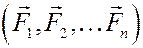называется плоской, если все её силы расположены в одной и той же плоскости.

Для плоской системы сил вычисление момента силы можно упростить: если центр О плоскости сил, то вектор момента обязательно 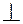этой плоскости.

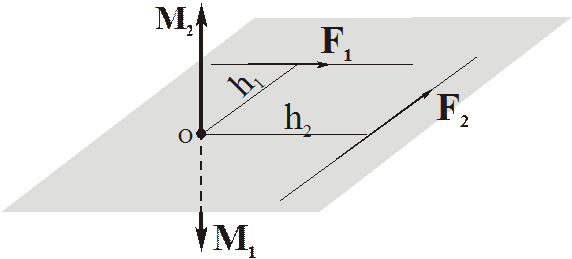
Следовательно, нужно указать только направление: к наблюдателю, или – от наблюдателя.

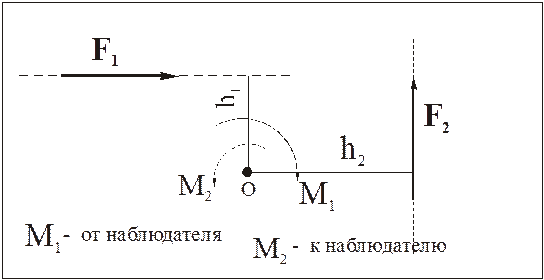
А это можно сделать, присваивая знак модулю момента: знак «+», если вектор направлен к наблюдателю, и знак «–», если – от наблюдателя.

Выражение

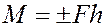
называется алгебраическим моментом силы относительно центра.

Алгебраический момент используется для определения вектора момента в случае плоской системы сил.

Знак «+» присваивается алгебраическому моменту, если сила стремится повернуть тело вокруг центра О против хода часовой стрелки (вектор момента направлен к наблюдателю). Знак «–» – если по часовой стрелке (вектор момента направлен от наблюдателя).

2. Момент силы относительно оси.

Моментом силы относительно ос и 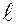называется проекция на эту ось вектора момента силы относительно какой-либо точки оси.

Если через обозначить единичный вектор оси, то

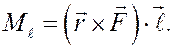
Проекция вектора момента силы на ось не зависит от выбора точки на оси. Действительно, используем тождество, справедливое для любых векторов:

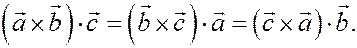
Тогда

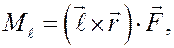
но ясно, что

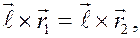
т.к. векторы совпадают по направлению и модули их равны:

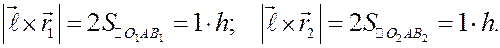
Следовательно,

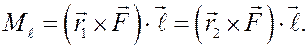
В отличие от момента силы относительно центра момент силы относительно оси – скалярная величина (проекция вектора на ось).

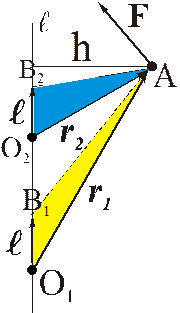
Для практического вычисления момента относительно оси формула (7) не удобна. Поэтому применяют следующее правило.

Чтобы найти момент силы относительно оси,

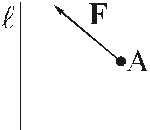нужно:

1) выбрать плоскость, перпендикулярную оси;

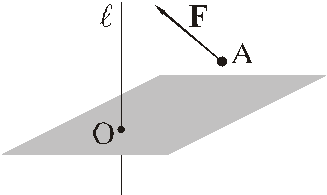
2) спроектировать силу на эту плоскость;

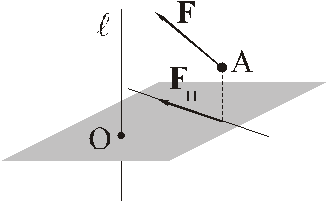
3) вычислить алгебраический момент полученной проекции относительно точки пересечения оси и плоскости.

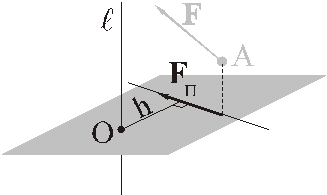
Этот алгебраический момент и будет моментом исходной силы относительно оси. Таким образом

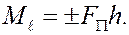
Замечание. При определении знака алгебраического момента следует смотреть с положительного направления оси, определяемого единичным вектором .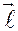

Приведённое правило справедливо для любой оси, в том числе и для координатных осей x, y, z. Но для координатных осей можно применять и формулы (3): по определению это и будут моменты силы относительно координатных осей (точка О всем трём осям).

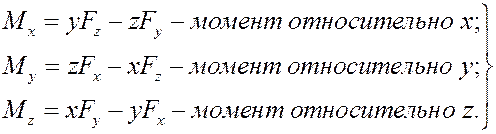
3. Понятие пары сил. Момент пары. Действия с парами сил.

К понятию пары сил пришли в результате анализа сложения двух параллельных сил. Две параллельные одинаково направленные силы имеют равнодействующую. Её модуль равен сумме модулей сил, направление совпадает с направлениями сил, а точка приложения делит внутренним образом отрезок между точками приложения сил на отрезки, обратно пропорциональные модулям сил.

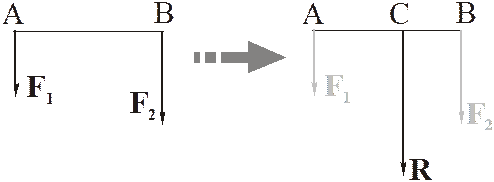
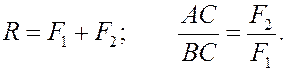
Такая же ситуация для двух параллельных, не равных по модулю и противоположно направленных сил. Если, например, 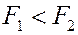, то

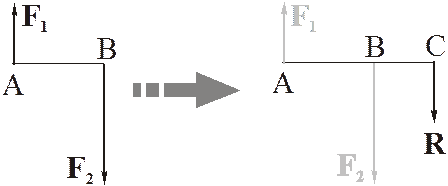
равнодействующая направлена в сторону большей по модулю силы, её модуль равен разности модулей сил, а точка приложения делит внешним образом отрезок АВ на отрезки обратно пропорциональные модулям сил:

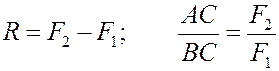
Теперь представим, что 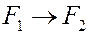. Тогда

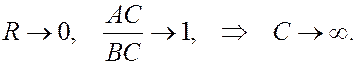
Следовательно, если силы параллельны, равны по модулю и противоположны по направлению, то равнодействующей не существует!

Две равные по модулю, противоположно направленные силы и параллельные силы называются парой сил.

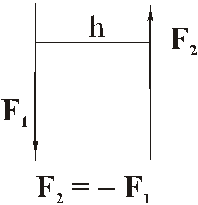
Расстояние между линиями действия сил пары называется плечом пары сил.

Пара сил не имеет равнодействующей. Её нельзя заменить одной силой!

Теорема. Сумма моментов сил пары относительно любого центра не зависит от этого центра.

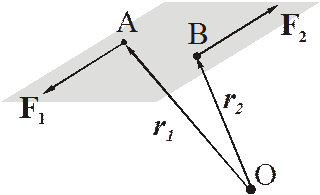
Имеем:

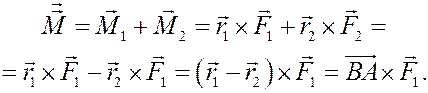
Если в сумме моментов заменить силу на 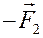, то аналогичным образом получим

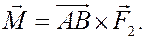
Таким образом, любое упоминание центра О из суммы моментов пропадает. чтд

Вектор, равный

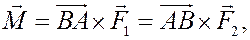
называется моментом пары сил.

Согласно (9)

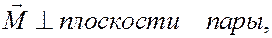
направлен так, что с его конца вращение пары происходит против часовой стрелки. Модуль момента пары

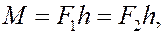
где h – плечо пары сил.

Преобразования, которые можно производить с парами сил, определяются двумя теоремами.

Теорема 1 (об эквивалентности пар сил). Любую пару сил, не изменяя её действия на тело, можно

1) перенести в любое место в плоскости пары;

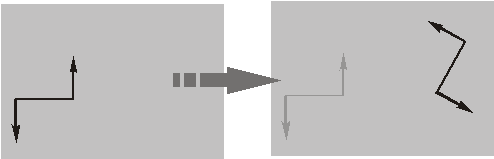
2 ) перенести в любую параллельную плоскость;

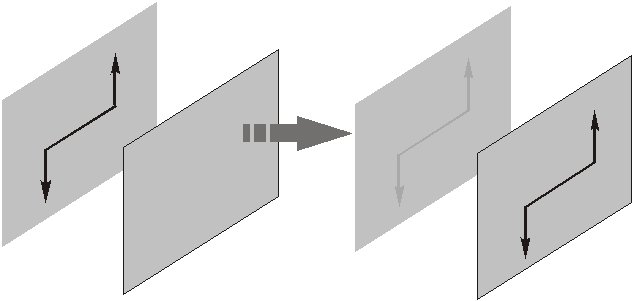
3) любым образом изменять плечо и модули сил пары, сохраняя постоянным их произведение.

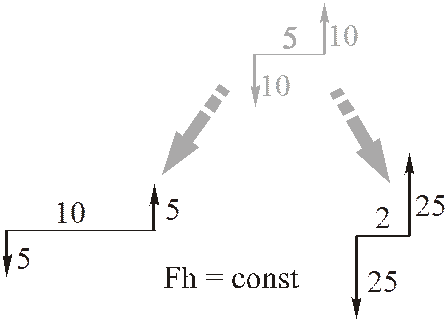
Следствие. Момент пары является свободным вектором.

Благодаря пункту 3) теоремы, пары сил можно изображать следующим образом.

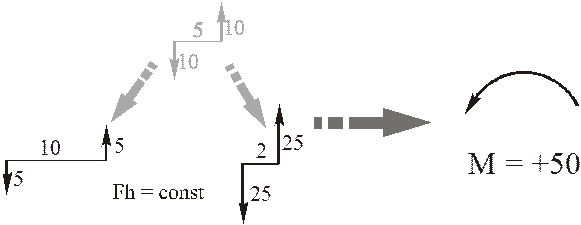
Замечание. Направление вектора момента пары обязательно должно сохраняться, т.е. моменты у эквивалентных пар должны быть равны как векторы.

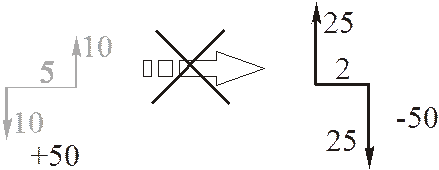
Теорема 2 (о сложении пар сил). Любая совокупность пар сил эквивалентна одной паре, момент которой равен векторной сумме моментов всех пар системы.

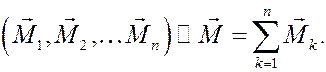
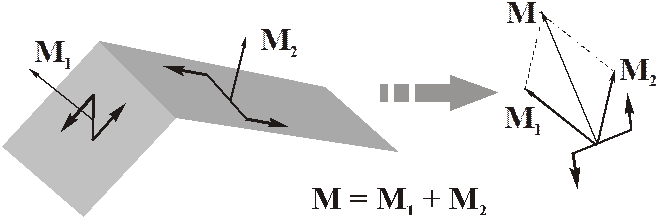
Пример.

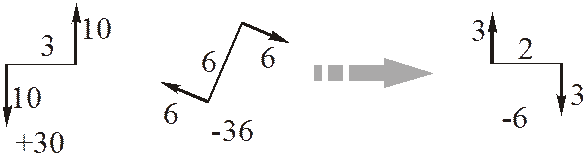
Дата добавления: 2014-01-20