Диференціальне формулювання закону Ома

Тепер повернемось знову до закону Ома 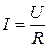і виразу для опору провідника, який ми записали у вигляді

,

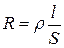приказуючи, що наведена формула справедлива для однорідних провідників , у яких переріз всюди один і той же 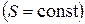. Ця формула є інтегральною. На практиці треба мати справу з провідниками довільної форми і з розподіленим питомим опором, отже для розв’язку задач, в яких можуть змінюватись 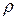і , і вздовж провідника, треба перейти до диференціальних співвідношень.

Для цього візьмемо трубку струму нескінченно малої довжини 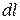і нескінченно малого перерізу 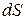, в межах якої питомий опір залишається сталим. По трубці тече струм 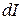, падіння напруги на трубці , при цьому струм протікає від точок з більшим потенціалом до точок з меншим потенціалом, тому 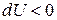, опір трубки .

Тоді за законом Ома для трубки

.

Скористаємось тим, що 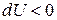, тоді

.

Але не що інше, як градієнт потенціалу вздовж трубки, тоді , де 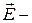поле в провіднику в точці, де знаходиться трубка (воно є векторною величиною, оскільки градієнт – вектор).

За означенням густина струму, тому

.

Скориставшись тим, що питома провідність, запишемо остаточно

закон Ома в диференціальному вигляді. Це рівняння, що встановлює зв’язок між густиною струму у провіднику і напруженістю електричного поля в ньому, являє собою найбільш загальне і просте формулювання закону Ома. Воно має назву диференціального, хоч і не містить похідних, оскільки встановлює зв’язок між величинами, що відносяться до однієї конкретної точки провідника. Величини , що визначені в кожній точці, можуть змінюватись від точки до точки, при цьому рівність 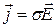зберігається. В ізотропних середовищах є скаляром, в анізотропних середовищах – тензором.

Дата добавления: 2014-01-20