Приклади на визначення опору

(самостійно)

Одержаний диференціальний вираз 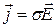дозволяє вирішувати задачі по знаходженню опору у випадках, коли формула 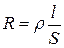не застосовна.

Сферичний конденсатор з провідністю речовини, що його заповнює.

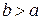Нехай є сферичний конденсатор з радіусами сфер і . Конденсатор заповнений речовиною з і питомим опором , що не залежить від координат . На самостійне опрацювання вам виносилось знайти хід потенціалу в такому конденсаторі

,

де , внутрішня сфера заземлена, на зовнішню відносно внутрішньої подається потенціал 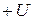. Струм тече від зовнішньої сфери до внутрішньої. Поле всередині конденсатору

,

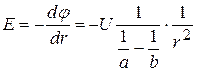густина струму

.

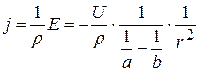Знак (–) показує, що струм тече в сторону зменшення 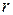. Враховуючи це і цікавлячись тільки абсолютним значенням величини , можемо цей знак випустити

.

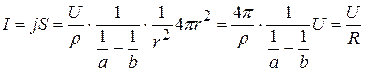Звідси

. в системі CGSE

Цей результат отриманий в системі CGSE. В системі СІ

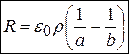. в системі СІ

Циліндричний конденсатор.

Позначимо радіус внутрішнього електроду , радіус зовнішнього електроду , внутрішній електрод заземлений, зовнішній електрод має потенціал 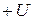. Розподіл потенціалу у циліндричному конденсаторі має вигляд

.

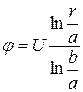Тоді поле у конденсаторі

.

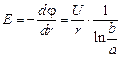Густина струму

.

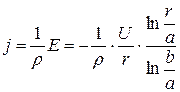Відкинемо знак “мінус”, і запишемо повний струм як , де довжина конденсатору. Підставивши значення густини струму у рівняння для струму, отримаємо опір

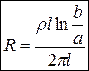. в системі CGSE

. в системі СІ

Дві провідні сфери у слабо провідному середовищі.

Дві провідні сфери радіусом знаходяться на відстані одна від одної в слабо провідному середовищі з питомим опором 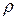. Ця задача моделює заземлення у лініях зв’язку, тобто заземлення одного з полюсів джерела струму і одного з вхідних проводів приймача.

Візьмемо сферичний конденсатор, для якого

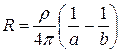
і спрямуємо до . Тоді

,

і опір визначається тільки радіусом . Для двох сфер

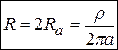в системі CGSE,

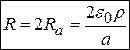в системі CGSE,

і не залежить від відстані між сферами при .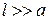

Дата добавления: 2014-01-20