Теория клубов. Оптимальные размеры клуба

Выбор по максимальному значению

Выбор по максимальному значению пытается учесть различную интенсивность предпочтений избирателей. Поэтому альтернати­вам приписывается соответствующий удельный вес. Максималь­ное значение может использоваться далеко не всеми участниками. В нашем случае (см. табл. 5.19) наиболее высокие баллы поставле­ны лишь первой группой избирателей.

Таблица 5.19

Выбор по максимальному значению (10-балльная система)

Группа I (6 избирателей)	Группа II (5 избирателей)	Группа III (4 избирателя)
А Б В Г		Б А Г В		В Г Б А

Распределение голосов: А -73, Б – 69, В – 47, Г – 32. Победил кандидат А.

Такая ситуация легко поддается манипулированию путем за­вышения интенсивности своих предпочтений. Это особенно легко сделать, зная предпочтения других. В нашем примере победите­лем оказывается А, хотя девять избирателей из 15 оценивали Б выше, чем А.

Рассмотренные нами процедуры голосования представляются довольно сложными и трудоемкими. Они обычно используют­ся лишь в малых группах. Применение их в более широких масштабах связано с резким ростом издержек, которые не может себе позволить представительная демократия. Впрочем, там есть свои особенности конкурентной борьбы, которые будут проана­лизированы в лекции 6. Однако прежде кратко остановимся на теории клубов.

Теория клубов описывает сообщества людей, объединяющихся с целью совместного потребления общественных благ. Их члены выступают во внешнем вполне «рыночном» мире как обычные покупатели общественных благ, а во внутренней сфере ограничивают доступ потенциальных потребителей к ним, обусловливая его необходимостью вступления в ряды членов клуба, одновременно сокра­щая индивидуальные затраты таких членов на получение подоб­ных клубных благ. Блага, потребляемые внутри клуба, одновре­менно содержат черты и общественных, и частных благ (так, свой­ством неисключаемости в потреблении обладают только члены клуба) и относятся к категории исключаемых общественных благ. Пусть в учреждаемом клубе полезность репрезентативного индивида определена на частном благе X и общественном благе G. Если размер (число членов) клуба N, то U = U(X, G, N). Пусть из­держки предоставления общественного блага клубу включают фиксированные издержки F, а цена единицы блага равна P_g. По­ложим, что каждый индивид получает не только одну и ту же функцию полезности U, но и одинаковый доход Y и каждый пла­тит один и тот же членский взнос t. Чтобы ответить на вопросы, какой уровень общественного блага необходим и каким должно быть число членов учреждаемого клуба, мы предполагаем, что по­лезность репрезентативного члена клуба максимизируется. Эта цель может появляться как добровольный выбор основателей клуба или как результат конкуренции. Когда существует конку­ренция за членство, любой клуб, не максимизирующий за счет технологий поставки исключаемых благ полезность своих чле­нов, не сможет выжить. Принимая во внимание бюджетное огра­ничение, получаем следующий лагранжиан:

L = U(X,G,N) + X(Y-P_xX-t). (5-1)

Если клуб действует при сбалансированном бюджетном огра­ничении, то t должен удовлетворять условию

tN = F + P_gG. (5-2)

Подставляя это выражения для замены t в (5-1), получаем:

L = U(X, G, N)+ λ(Y - P_xX - F/N - P_gG/N). (5-3)

Максимизируя (5-3) no X, G, и N, получаем условие первого порядка:

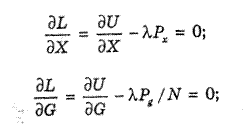(5-4), (5-5)

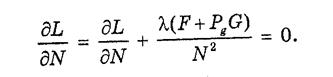(5-6)

Из (5-4) и (5-5) получаем

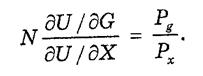(5-7)

Количество общественных благ для членов клуба должно выбираться так, чтобы выполнялось условие Самуэльсона для Парето-оптимального обеспечения, т. е. сумма предельных норм замещения общественных благ частными для всех членов клуба должна равняться отношению их цен. Из (5-5) и (5-6) получаем

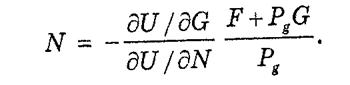(5-8)

Если расширение клуба приводит к нежелательному переполнению (перегруженности), ∂ U / ∂N < 0, и (5-8) дает N > 0. Чем больше неудобства и выше издержки из-за перегруженности по отношению к предельной полезности общественного блага, тем меньше оптимальный размер клуба. Чем больше постоянные издержки обеспечения общественных благ членам клуба, тем больше оптимальный размер клуба из-за возможности разделять издержки на большее число участников (рис. 5.3).

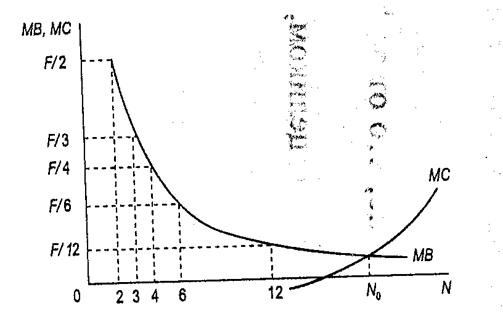
Рис. 5.3. Определение оптимального размера клуба

Дата добавления: 2014-01-20