
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
ВВЕДЕНИЕ. Преобразование Лапласа
|
|
|
|
Преобразование Лапласа
ЛЕКЦИЯ № 1
Учебная цель: дать понятие об общих принципах операционного исчисления, формировать знания о преобразовании Лапласа функций ограниченного роста, об обратном преобразовании Лапласа, об оригинале и изображении.
Учебные вопросы:
1. Преобразование Лапласа функций ограниченного роста.
2. Простейшие свойства преобразования Лапласа.
3. Теоремы подобия, смещения, запаздывания.
Литература:
1. Пискунов Н.С. Дифференциальное и интегральное исчисления для ВТУЗов. Т.2, гл.19.
Операционное исчисление (ОИ) – одна из важнейших областей математического анализа. Методы ОИ используются в физике, механике, электротехнике и других науках при решении различных вопросов. Особенно широкое применение ОИ имеет в автоматике и телемеханике.
Еще в 19 веке математики начали заниматься так называемым символическим исчислением, в котором проводятся формальные операции над величиной р, которая является символом дифференцирования, например, если есть функция  , то умножение
, то умножение  означает дифференцирование функции
означает дифференцирование функции  :
:
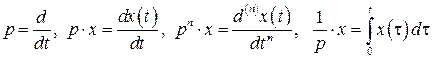
Популяризации символического исчисления в значительной степени способствовал английский инженер Хевисайд, который успешно применял его в решении дифференциальных уравнений, связанных с различными электрическими процессами. Однако он не заботился о строгом математическом обосновании метода, что иногда приводило к неверным результатам.
Строгое математическое обоснование метода появилось лишь в 20-е годы 20 века. В основе его лежит так называемое преобразование Лапласа. Суть этого метода заключается в следующем. Операции дифференцирования и интегрирования заменяются некоторыми алгебраическими операциями. В результате дифференциальное уравнение заменяется алгебраическим. Находится алгебраическое решение, а по нему восстанавливается искомое решение дифференциального уравнения.
Вопрос 1. Преобразование Лапласа функций ограниченного роста.
Определение 1. Комплекснозначная функция 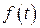 вещественного аргумента t называется функцией ограниченного роста с показателем l, если она по модулю возрастает не быстрее некоторой показательной функции, т.е.
вещественного аргумента t называется функцией ограниченного роста с показателем l, если она по модулю возрастает не быстрее некоторой показательной функции, т.е.
1) существует такое число М (зависящее от функции f), что  ,
, 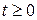 ;
;
2)  ;
;
3) функция 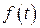 кусочно-непрерывно дифференцируема на всей числовой оси и на каждом конечном промежутке она имеет конечное число точек разрыва 1-го рода.
кусочно-непрерывно дифференцируема на всей числовой оси и на каждом конечном промежутке она имеет конечное число точек разрыва 1-го рода.
График такой функции может выглядеть, например, так:
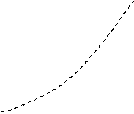
 у
у
 |

 |


 М
М
 | |||
 |

 0
0 
 t
t


 – М
– М
 |

Поскольку функции ограниченного роста при 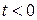 заведомо принимают нулевые значения, в дальнейшем мы будем задавать их аналитические выражения только при
заведомо принимают нулевые значения, в дальнейшем мы будем задавать их аналитические выражения только при 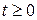 , не оговаривая это специально.
, не оговаривая это специально.
Например, вместо полного определения функции  будем использовать краткую запись
будем использовать краткую запись  , позволяющую утверждать, что
, позволяющую утверждать, что 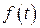 – функция ограниченного роста с показателем
– функция ограниченного роста с показателем  .
.
Другой пример:  .
.
Определение 2. Множество всех функций ограниченного роста с показателем l называется пространством функций ограниченного роста с показателем l и обозначается  .
.
Хотя пространства  включают в себя наиболее употребительные типы функций, многие функции не входят ни в одно из этих пространств.
включают в себя наиболее употребительные типы функций, многие функции не входят ни в одно из этих пространств.
Например, функция  не является функцией ограниченного роста, поскольку при любых l и
не является функцией ограниченного роста, поскольку при любых l и 
 .
.
Функция  , где
, где  , также не принадлежит
, также не принадлежит  , ввиду имеющегося разрыва 2-го рода в точке
, ввиду имеющегося разрыва 2-го рода в точке 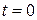 .
.
 Теорема 1. Если функция
Теорема 1. Если функция  , то зависящий от комплексного параметра р несобственный интеграл
, то зависящий от комплексного параметра р несобственный интеграл  абсолютно сходится при всех р, удовлетворяющих условию
абсолютно сходится при всех р, удовлетворяющих условию  .
.
Доказательство.
Пусть р – комплексное число,  .
.
Оценим величину  :
:
 ,
,  ,
,

 ,
,
 (по определению 1),
(по определению 1),  .
.
Итак,  .
.
По условию  , тогда
, тогда  .
.
Вычислим несобственный интеграл
 ,
,
т.е. интеграл сходится.
По признаку сравнения для несобственных интегралов от положительных функций из сходимости интеграла от большей функции следует сходимость интеграла от меньшей функции, следовательно, сходится интеграл  , а значит, исходный интеграл
, а значит, исходный интеграл  сходится абсолютно.
сходится абсолютно.
Определение 3 (определение преобразования Лапласа). Пусть  – пространство функций ограниченного роста с показателем l, функция
– пространство функций ограниченного роста с показателем l, функция  ; домножим ее на
; домножим ее на  , где р – некоторое комплексное число и проинтегрируем по t от 0 до ¥:
, где р – некоторое комплексное число и проинтегрируем по t от 0 до ¥:
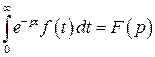 . (1)
. (1)
Функция 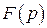 называется преобразованием Лапласа функции
называется преобразованием Лапласа функции 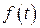 .
.
Функция 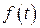 (удовлетворяющая условиям 1) – 3)) называется оригиналом (прообразом), а функция
(удовлетворяющая условиям 1) – 3)) называется оригиналом (прообразом), а функция 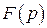 – изображением Лапласа функции
– изображением Лапласа функции 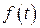 (или, короче, изображение, образ).
(или, короче, изображение, образ).
Обозначения:
 или
или 
Примеры нахождения изображений
1. Рассмотрим функцию  . Функция
. Функция  называется единичной функцией Хевисайда.
называется единичной функцией Хевисайда.
    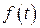 0 t
0 t
|  .
Итак, .
Итак,  , причем функция , причем функция 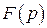 определена в области определена в области  . .
|
2. Рассмотрим функцию  , где а – комплексное число.
, где а – комплексное число.
Имеем:  , если
, если  или
или  (т.е. правее прямой
(т.е. правее прямой  ).
).
Итак 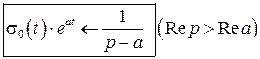 .
.
Роль множителя  в левой части состоит в том, что он «гасит» (обращает в нуль) функцию при
в левой части состоит в том, что он «гасит» (обращает в нуль) функцию при 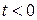 . В дальнейшем будем считать, что все рассматриваемые нами функции снабжены множителем
. В дальнейшем будем считать, что все рассматриваемые нами функции снабжены множителем  , хотя сам этот множитель в написании часто будем опускать.
, хотя сам этот множитель в написании часто будем опускать.
3. Рассмотрим функцию  .
.
Имеем: 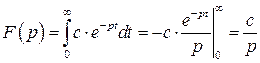 . Итак,
. Итак,  .
.
Вопрос 2. Простейшие свойства преобразования Лапласа.
 |
Теорема (о единственности изображения).
Если две непрерывные функции  и
и 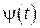 имеют одно и то же изображение, то эти функции тождественно равны:
имеют одно и то же изображение, то эти функции тождественно равны: 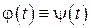 .
.
 |
|
|
|
|
|
Дата добавления: 2014-01-20; Просмотров: 706; Нарушение авторских прав?; Мы поможем в написании вашей работы!