С постоянными коэффициентами и их систем

Операторный метод решения линейных дифференциальных уравнений

ЛЕКЦИЯ № 3

Оптическое стекло. Его характеристики

Для оптических приборов применяются специальные оптические стекла, которые характеризуются показателем преломления и дисперсией для лучей света, дающих следующие спектральные линии: 1) желтую линию натрия, совпадающую с линией Б Фраунгофера в спектре поглощения от лучей солнца; 2) три яркие линии водорода, из которых две совпадают с линиями F и С Фраунгофера.

Оптическое стекло в зависимости от его состава и оптических свойств по ГОСТ 3514—51 подразделяется на две основные группы: кроны и флинты и каждая из них — на подгруппы—марки. Марка стекла обозначается буквой, характеризующей данную подгруппу, которой принадлежит стекло, и порядковым номером стекла/

Кроновыми называются стекла без содержания в них окиси свинца или с малым содержанием (не более 3%), содержат до 60% SiO₂(кварц) (показатель преломления 1.47..1.66), а флинтовыми — со значительным содержанием окиси свинца, содержат до 40% SiO₂(более мягкое, показатель преломления 1.63..1.66).

Оптические стекла характеризуются следующими показателями качества: коэффициентом светопоглощения, оптической однородностью, пузырностью, двойным лучепреломлением. Кроме этого, стекла характеризуются химическими свойствами: способностью противостоять разрушению водой, растворами кислот и щелочей, газами атмосферы и др.; механическими свойствами: плотностью стекла, прочностью, твердостью и хрупкостью; термическими свойствами: коэффициентом линейного расширения, температурным приращением показателя приращения.

Показатель преломления возрастает при нагревании стекла. Он может изменяться на 1—2 единицы шестого знака для стекол с показателем преломления около 1,5 и на 1—3 единицы пятого знака для стекол с показателем преломления 1,7—1,9 при изменении температуры на 1 градус С. Бывают стекла следующих сортов: кроны, баритовые кроны, крон флинты, баритовые флинты, легкие флинты, тяжелые кроны, флинты, тяжелые флинты (по содержанию свинца).

Учебные вопросы:

1. Решение задачи Коши для линейного дифференциального уравнения с постоянными коэффициентами операторным методом.

2. Решение задачи Коши для системы линейных дифференциальных уравнений с постоянными коэффициентами операторным методом.

Литература:

1. Пискунов Н.С. Дифференциальное и интегральное исчисления для ВТУЗов. Т.2, гл.19.

Вопрос 1. Решение задачи Коши для линейного дифференциального уравнения с постоянными коэффициентами операторным методом.

Применим общую схему решения функциональных уравнений операторным методом к задаче Коши для линейного уравнения с постоянными коэффициентами.

Ограничимся рассмотрением уравнений 2-го порядка.

Пусть требуется найти решение задачи Коши:

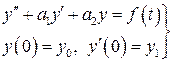. (1)

Будем предполагать, что функция является непрерывной функцией ограниченного роста с показателем λ, .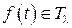

Будем искать решение 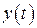среди дважды дифференцируемых функций также принадлежащих .

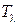Обозначим изображение искомого решения 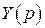, т.е. .

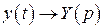Запишем изображение производных:

,

.

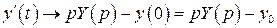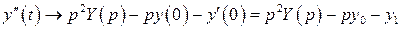Пусть .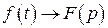

Подставим это в уравнение (1) и от ДУ (в оригиналах) перейдем к алгебраическому уравнению (в изображениях).

, (2)

Алгебраическое уравнение относительно изображения 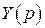искомой функции (2) называют операторным уравнением (или уравнением, изображающим уравнение задачи (1)). Решая его, найдем операторное решение задачи:

–

– изображение искомого решения.

Дата добавления: 2014-01-20